$\color{green}{<–画图不易，点下这里赞一下吧}$

迪杰斯特拉算法采用的是一种贪心的策略。

求源点到其余各点的最短距离步骤如下：

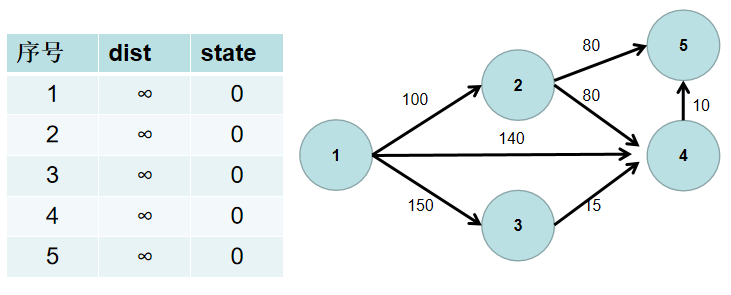
1. 用一个 dist 数组保存源点到其余各个节点的距离，dist[i] 表示源点到节点 i 的距离。初始时，dist 数组的各个元素为无穷大。
   用一个状态数组 state 记录是否找到了源点到该节点的最短距离，state[i] 如果为真，则表示找到了源点到节点 i 的最短距离，state[i] 如果为假，则表示源点到节点 i 的最短距离还没有找到。初始时，state 各个元素为假。
   {:weith=150 height=150}

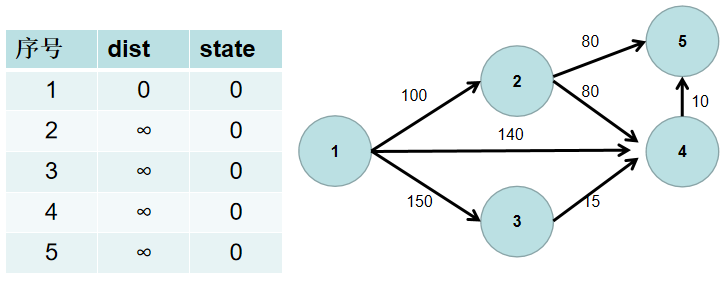
2. 源点到源点的距离为 0。即dist[1] = 0。
   {:weith=150 height=150}

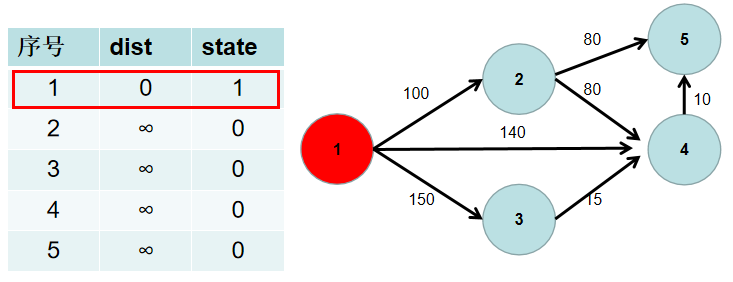
3. 遍历 dist 数组，找到一个节点，这个节点是：没有确定最短路径的节点中距离源点最近的点。假设该节点编号为 i。此时就找到了源点到该节点的最短距离，state[i] 置为 1。
   {:weith=150 height=150}

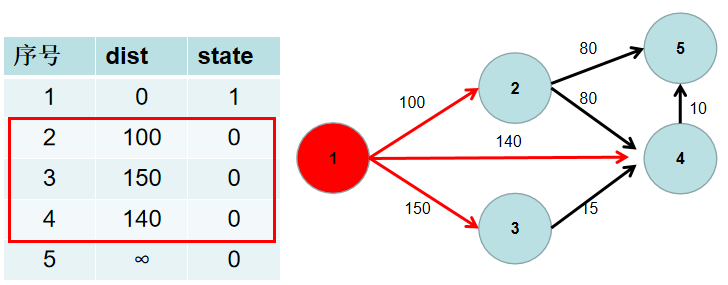
4. 遍历 i 所有可以到达的节点 j，如果 dist[j] 大于 dist[i] 加上 i -> j 的距离，即 dist[j] > dist[i] + w[i][j]（w[i][j] 为 i -> j 的距离） ，则更新 dist[j] = dist[i] + w[i][j]。
   {:weith=150 height=150}

5. 重复 3 4 步骤，直到所有节点的状态都被置为 1。
   

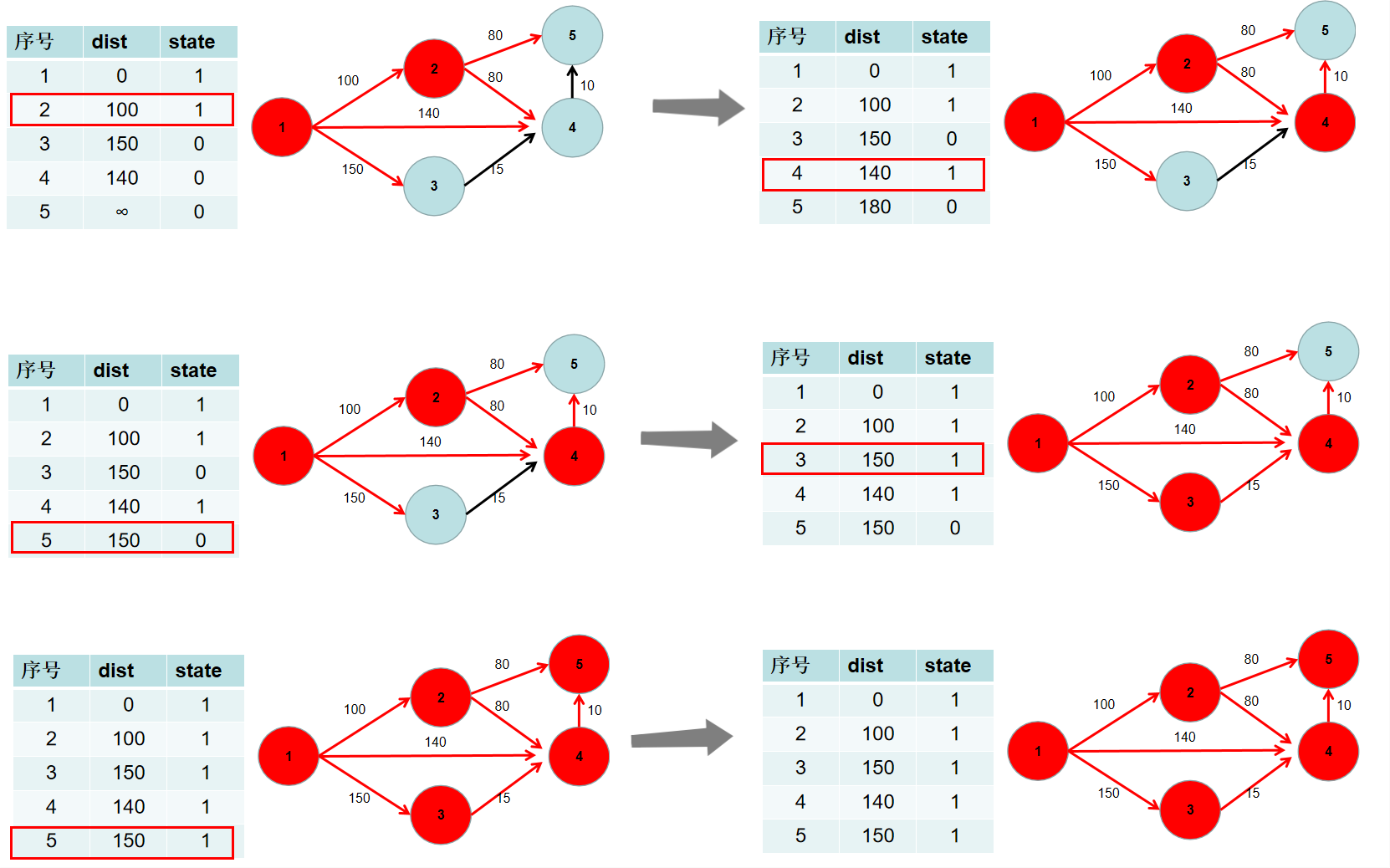
6. 此时 dist 数组中，就保存了源点到其余各个节点的最短距离。
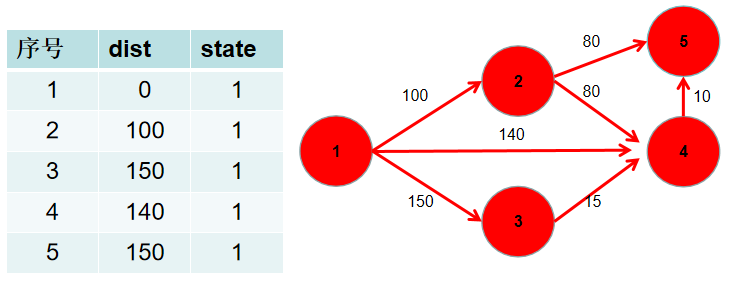   {:weith=150 height=150}

伪代码：

int dist[n],state[n];
dist[1] = 0, state[1] = 1;
for(i:1 ~ n)
{
    t <- 没有确定最短路径的节点中距离源点最近的点;
    state[t] = 1;
    更新 dist;
}

#include<iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510, M = 100010;

int h[N], e[M], ne[M], w[M], idx;//邻接表存储图
int state[N];//state 记录是否找到了源点到该节点的最短距离
int dist[N];//dist 数组保存源点到其余各个节点的距离
int n, m;//图的节点个数和边数

void add(int a, int b, int c)//插入边
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void Dijkstra()
{
    memset(dist, 0x3f, sizeof(dist));//dist 数组的各个元素为无穷大
    dist[1] = 0;//源点到源点的距离为置为 0
    for (int i = 0; i < n; i++)
    {
        int t = -1;
        for (int j = 1; j <= n; j++)//遍历 dist 数组，找到没有确定最短路径的节点中距离源点最近的点t
        {
            if (!state[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        }

        state[t] = 1;//state[i] 置为 1。

        for (int j = h[t]; j != -1; j = ne[j])//遍历 t 所有可以到达的节点 i
        {
            int i = e[j];
            dist[i] = min(dist[i], dist[t] + w[j]);//更新 dist[j]
        }


    }
}

int main()
{
    memset(h, -1, sizeof(h));//邻接表初始化

    cin >> n >> m;
    while (m--)//读入 m 条边
    {
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);
    }

    Dijkstra();
    if (dist[n] != 0x3f3f3f3f)//如果dist[n]被更新了，则存在路径
        cout << dist[n];
    else
        cout << "-1";
}

优化

看一下算法的时间复杂度：

for(i:1 ~ n)//n次
{
    t <- 没有确定最短路径的节点中距离源点最近的点;//每次遍一遍历dist数组，n次的复杂度是O(n^2)
    state[t] = 1;
    更新 dist;//每次遍历一个节点的出边，n次遍历了所有节点的边，复杂度为O(e)
}

算法的主要耗时的步骤是从dist 数组中选出：没有确定最短路径的节点中距离源点最近的点 t。只是找个最小值而已，没有必要每次遍历一遍dist数组。

在一组数中每次能很快的找到最小值，很容易想到使用小根堆。可以使用库中的小根堆（推荐）或者自己编写。

代码：

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>//堆的头文件

using namespace std;

typedef pair<int, int> PII;//堆里存储距离和节点编号

const int N = 1e6 + 10;

int n, m;//节点数量和边数
int h[N], w[N], e[N], ne[N], idx;//邻接表存储图
int dist[N];//存储距离
bool st[N];//存储状态

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆
    heap.push({0, 1});//插入距离和节点编号

    while (heap.size())
    {
        auto t = heap.top();//取距离源点最近的点
        heap.pop();

        int ver = t.second, distance = t.first;//ver:节点编号，distance:源点距离ver 的距离

        if (st[ver]) continue;//如果距离已经确定，则跳过该点
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});//距离变小，则入堆
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}

//参考yxc

使用小根堆后，找到 t 的耗时从 O(n^2) 将为了 O(1)。每次更新 dist 后，需要向堆中插入更新的信息。所以更新dist的时间复杂度有 O(e) 变为了 O(e*logn)。总时间复杂度有 O(n^2) 变为了 O(n + e*longn)。适用于稀疏图。

总结

迪杰斯特拉算法适用于求正权有向图中，源点到其余各个节点的最短路径。注意：图中可以有环，但不能有负权边。

例如：如下图就不能使用迪杰斯特拉算法求节点 1 到其余各个节点的最短距离。
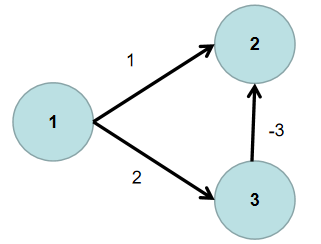{:weith=150 height=150}

求个点赞~~