题目描述
给定一个有序整数数组,元素各不相同且按升序排列,编写一个算法,创建一棵高度最小的二叉搜索树。
示例:
给定有序数组: [-10,-3,0,5,9],
一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树:
0
/ \
-3 9
/ /
-10 5
算法1
由于数组是递增有序数组
要求高度尽量小,等同于左右子树高度相同
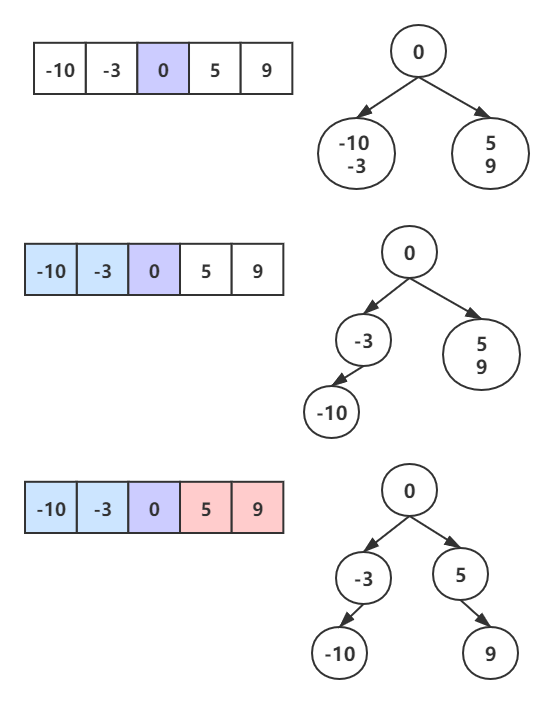
那么去中间的点为根节点(左右节点数相差最多为1)
左边部分再生成一个高度尽量小的子树
右边部分再生成一个高度尽量小的子树
即可
过程处理类似,数据规模逐步缩小
考虑使用递归解决
C++ 代码
class Solution {
public:
TreeNode* dfs(const vector<int>& nums, int l, int r) {
if (l > r) return NULL;
int mid = l + r >> 1;
TreeNode* root = new TreeNode(nums[mid]);
root->left = dfs(nums, l, mid-1);
root->right = dfs(nums, mid + 1, r);
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
TreeNode* root = dfs(nums,0, nums.size()-1);
return root;
}
};

