题目描述

题意：格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。格雷编码序列必须以 0 开头。

样例

Example 1:

Input: 2
Output: [0,1,3,2]
Explanation:
00 - 0
01 - 1
11 - 3
10 - 2

For a given n, a gray code sequence may not be uniquely defined.
For example, [0,2,3,1] is also a valid gray code sequence.

00 - 0
10 - 2
11 - 3
01 - 1

Example 2:

Input: 0
Output: [0]
Explanation: We define the gray code sequence to begin with 0.
             A gray code sequence of n has size = 2n, which for n = 0 the size is 20 = 1.
             Therefore, for n = 0 the gray code sequence is [0].

这道题其实不难，但是由于格雷码之前离散数学，组合数学上面都讲过，所以总结一下。
设想我们利用二进制编码去生成一个集合的幂集，如果按照二进制编码去生成最终的集合相邻两个集合变化会很大，但是如果使用格雷码去生成一个集合的幂集就可以保证相邻两个集合最多相差一个元素。

算法1

(递归)

题解1:我们可以观察到假设我们生成了k位比特的格雷码，在生成k + 1位格雷码时，首先顺序将所有的k位格雷码前面添上0（十进制值保持不变），然后逆序将所有的k位格雷码前面添上1（加上1 << k）。

C++ 代码

class Solution {
public:
    vector<int> grayCode(int n) {
        vector<int> res;
        res.push_back(0);
        int t = 1,size = 1;
        for(int k = 0 ; k < n ; k ++)
        {
            vector<int> cur;
            for(int i = 0 ; i < size ;i ++)
                cur.push_back(res[i]);
            for(int i = size - 1; i >= 0 ; i --)
                cur.push_back(res[i] + t);
            res = cur;
            size = res.size();
            t = t << 1;
        }
        return res;
    }
};

算法2

(异或生成)

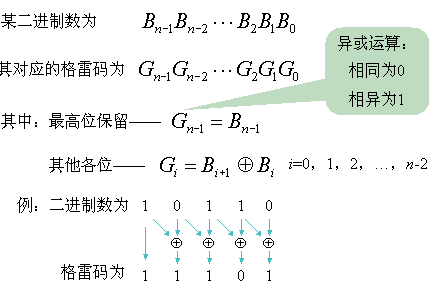
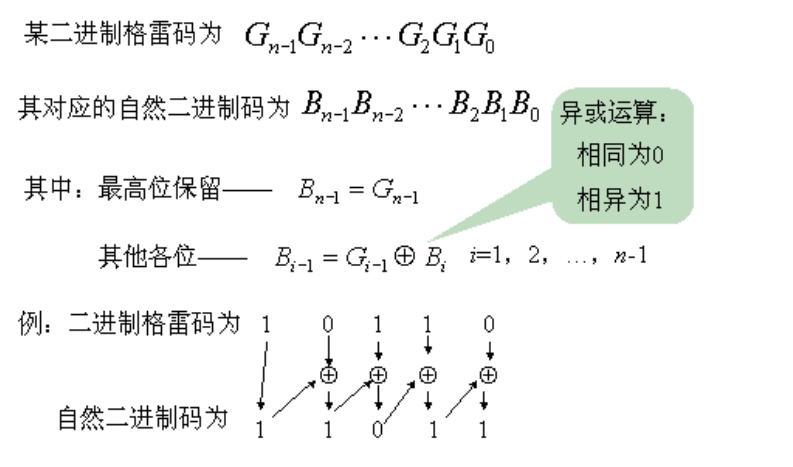
题解2:根据二进制数与格雷码的转化关系。

    vector<int> grayCode(int n) {
        int count = 1 << n;
        vector<int> res(count,0);
        for(int i = 1 ; i < count; i ++)
        {
            int bin = i,cur = bin >> (n - 1);
            for(int k = n - 1;k > 0;k --)
                cur = (cur << 1) + (((bin >> k) & 1) ^ ((bin >>(k - 1)) & 1));
            res[i] = cur;
        }
        return res;
    }

算法3

(迭代构造方式)

题解三：格雷码另一种生成方式：从000开始，重复进行如下两步直至全部生成

• 改变最右边的位的值
• 改变从右边开始第一个1左边元素的值。

000.  001.   011.  010.  110. 111. 101. 100.

class Solution {
public:
    vector<int> grayCode(int n) {
        int count = 1 << n;
        vector<int> res(count,0);
        for(int i = 1 ; i < count; i ++)
        {
            int cur = res[i - 1];
            if(i % 2 == 1)
                cur  = cur ^ 1;
            else
            {
                int k = 0;
                while(((cur >> k) & 1) == 0) 
                    k ++;
                cur = cur ^ (1 << (k + 1));
            }
            res[i] = cur;
        }
        return res;
    }
};