题目描述

You are given an array nums and an integer k. The XOR of a segment [left, right] where left <= right is the XOR of all the elements with indices between left and right, inclusive: nums[left] XOR nums[left+1] XOR ... XOR nums[right].

Return the minimum number of elements to change in the array such that the XOR of all segments of size k is equal to zero.

样例

[1, 2, 0, 3, 0], k = 1
Ouput: 3
[0, 0, 0, 0, 0] 改三个

y总最后一次周赛讲解

目录：
1. 找规律：发现是以k为周期
2. 分类讨论：①贪心
②DP

1 找规律

①^= 是按位异或。 同1为0. 一个1为1.
这里的意思是
[[a, …, ]…]

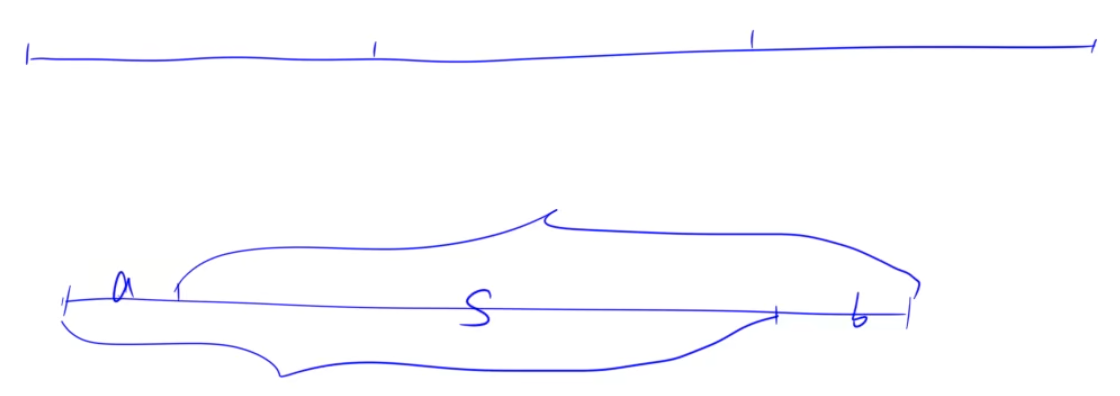
所以长度为k的子串s。a是其中一个，则有：
a & S = 0
同样子串s (后方)，b是后面一段，则有
b & S = 0
=> (a ^ s) ^ (b ^ s) = 0
=> (a ^ b) = 0
a = b
(因为S = a ^ num[i + 1] ^… = 0 所以多异或一个还是0)
(a ^ a ^ (…) = 0 ^ a = 0)

所以这个改完后的序列是以k为周期。
所有长度为k的周期折叠下来。
[a0 a1 …]
[a0 a1 …]
[ ]
[ ]
[a0 a1 …]
问：把每个位置上的数变相同，问操作多少次。每个区间独立。
变为众数。 (改的次数最少) ^= 0

2 分类讨论：

① 某一列用了一个全新的数
（贪心）直接用其他数异或结果res ^ res = 0
sum - 众数
综合讨论：
如果用原来的数：
操作数：si - maxvi (s表示和，mAxv表示众数，第i列)
变成任意数的话就会增加 mAxvi的操作数。
所以综合来看，选众数最少的一列即可。maxv = $\pi_{i = 0}^{n} min(mAxv_i)$

②每一列都用了原来的数

DP即可f(i, j) : 前i列异或和是j，它的总操作次数最少的数量。
枚举第i列的所有选法n^3. 但i*j两重循环乘到一块才是n=》$O(n^2)$

C++ 代码

class Solution {
public:
    const int M = 1024, INF = 1e8; //数值范围0~1023。共1024个数。
    int s[1024]; //每一列众数求的时候可用数组

    int minChanges(vector<int>& nums, int k){
        int n = nums.size(), m = (n + k - 1) / k; //n表示列（即元素）数量; m表示行数(长度为k的字段)
        vector<vector<int>> f(k + 1, vector<int>(M, INF)); //状态数组f[][] 第二维是数值大小。小于2^10 // 二进制表示中‘1’出现在前九位，最大异或1023. //都初始化为INF， （>2000即可）
        f[0][0] = 0; //只有0是合法方案。
        int sum = 0, minv = INF; //贪心解，总和，最小众数minv
        for (int i = 1; i <= k; i++){
            memset(s, 0, sizeof s); //先把s数组清空
            int len = m; //看这一列有多少个数 (最后一行可能不足k个数)
            if (n % k && n % k < i) len --; //如果是k长度，并且是<i 说明这一列在后面，这一行的数减一
        //枚举这一列的所有数
            for (int j = 0; j < len; j++)
                s[nums[j * k + i - 1]] ++ ;//原数组，下标从0开始，所以减一
            //求众数
            int maxv = 0;
            for (int j = 0; j < M; j++)
                if (s[j]) //s[j] >=0的话
                    maxv = max(maxv, s[j]); //更新众数
            sum += len - maxv; //行里的数总和 -众数。
            minv = min(minv, maxv); //选最小的众数
            //DP 
            for (int j = 0; j < M; j++)
                for (int u = 0; u < len; u++){
                    int x = nums[u * k + i - 1], cost = len - s[x]; //修改个数=总数-x数量
                    f[i][j] = min(f[i][j], f[i - 1][j ^ x] + cost);
                }
        }
    //最终两种①②情况取一个min
        return min(sum + minv, f[k][0]);
    }
};
这个不重要。

(贪心题和DP不能用特殊值证明(我觉得是泛化困难Generalisation, 除非神否则很难直觉看出/推出))
y总代码 视频讲解