算法模型：贪心 + dp

思想：分类讨论

由于题目要求的是任意长度为K的区间的异或和都为0，如果存在这样的两个区间seq[a,a+k-1]和seq[b,b+k-1]
其中a<b，异或运算的推导可以得到，这两个区间不重叠的部分是一样的，换句话说就是最终答案一定是以k为周期的序列 。

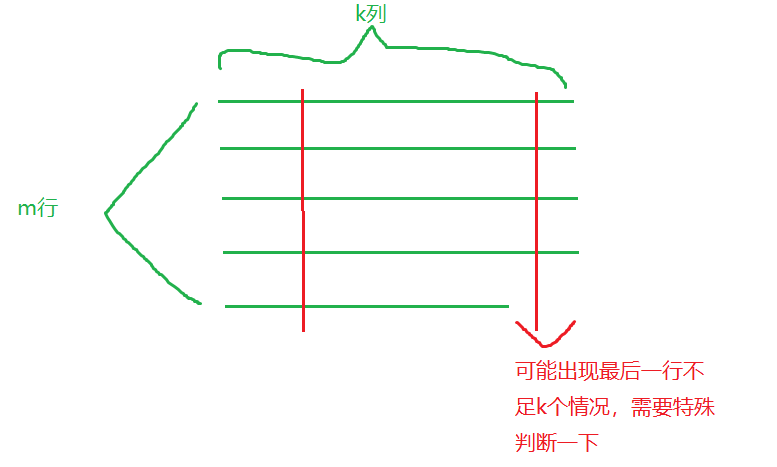
先考虑一种简单的情况，先将异或和为0的条件去掉，如何修改序列中的元素使得序列变成周期是k的序列，可以采用贪心的方法。在一个周期内，对于每一列来说是独立的，因此求出每一列元素的众数，然后修改行数-众数就是这列的最小的修改次数了。

然后我们想想怎么把异或和为0的限制加上，这里需要分情况讨论。第一种情况采用贪心的方法求得最优解。因为修改后的元素可能是原序列中没有出现过的元素。如果修改的某一列的元素是原序列中没有出现过的元素，那么这种情况下一定可以用贪心的办法求出最优解，做法是将众数最小的一列中的每个数变成一个全新的，该列中没有出现的，使得每个周期内的元素的异或和为0的数。第二种情况采用dp的方法求得最优解在这种情况下，由于没有最终修改后的元素是原数组中存在的数，因此可以从前往后枚举每一列，然后枚举选择第几行的数作为这列元素修改后的元素，由于异或具有交换性质，因此不具有顺序的问题，所以可以采用dp的方法递推出将序列变成数组中本来存在的某个数的情况。边界，f[0][0] = 0，目标状态是f[k][0]，状态表示f[i][j]为前i列异或和为j的情况下的最小值。

class Solution {
public:
    const int N = 1024, INF = 1e8;
    int s[1024];    //求众数的数组

    int minChanges(vector<int>& nums, int k) {
        int n = nums.size(), m = (n + k - 1) / k;
        vector<vector<int>> f(k+1,vector<int>(N,INF));

        int cnt = 0, minv = INF;
        f[0][0] = 0;    //边界：第0列只有异或和为0是合法的状态
        for(int i=1;i<=k;i++){
            int len = m;
            memset(s,0,sizeof s);
            if(n % k && n%k < i) len --;
            for(int j=0;j<len;j++){
                s[nums[j * k + i - 1]] ++;
            }
            int maxv = 0;
            for(int j=0;j<N;j++){
                maxv = max(maxv,s[j]);
            }
            cnt += len - maxv;
            minv = min(minv,maxv);
            for(int j=0;j<N;j++){
                for(int u=0;u<len;u++){
                    int x = nums[u*k+i-1];
                    f[i][j] = min(f[i][j],f[i-1][j^x] + len - s[x]);    //将x作为修改后的值
                }
            }
        }
        return min(cnt + minv, f[k][0]);    //返回贪心解和dp解的最小值
    }
};