写老题还能发现新方法, 代码复杂度还比其他的两次dfs快点
las 表示当前直径第一次是被节点las更新, cnt表示答案2
dp通过dfs找直径的时候, dfs维护一个当前节点最长路径的公共边的长度
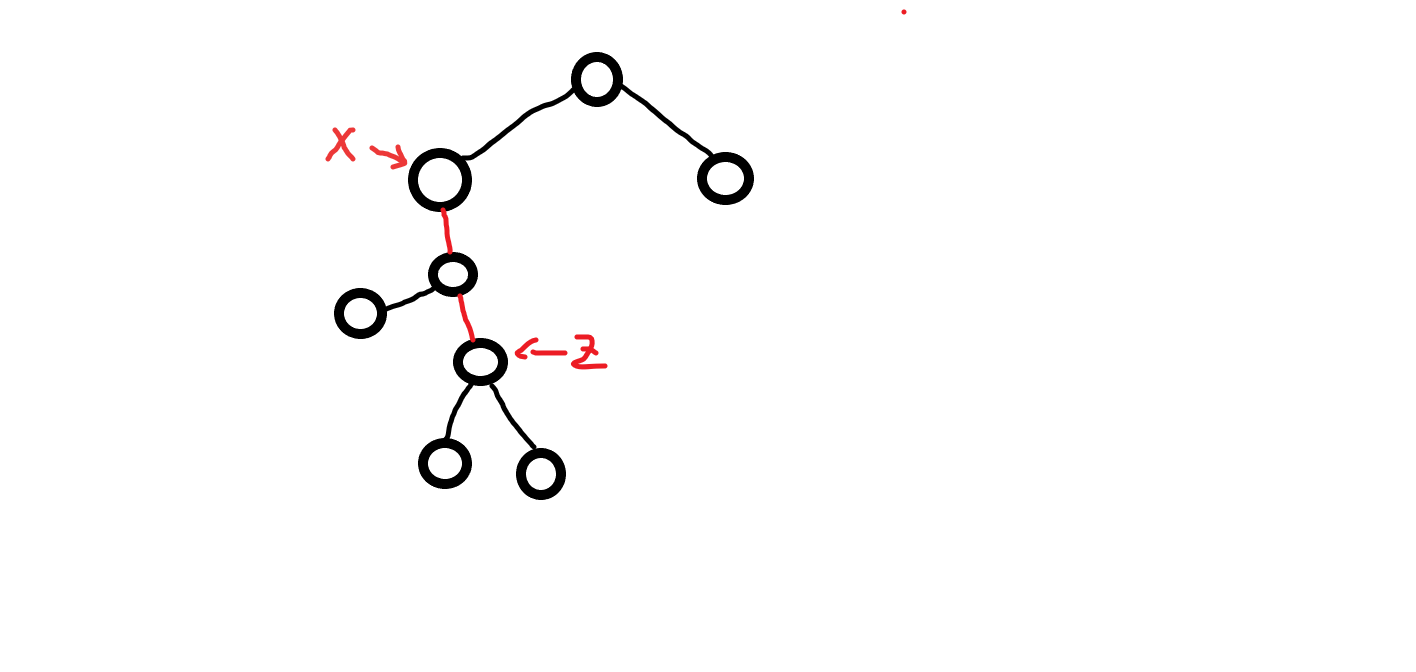
如图红色的边即为 x 到叶子节点最长路径的公共边, 为了方便计算
我们不记录公共边的数量, 而实记录dep[z], 通过 dep[x] - dep[z] 即可获得边数, res = dep[z]
看直径更新的时候的情况
- ans < d[x] + d[y] + cost(x, y), 更新 ans, las = x, cnt = res + cur - dep[x] * 2
- ans == d[x] + d[y] + cost(x, y)
las 不在 x 为根的子树当中, 那么当前的ans一定不是这棵树的直径, 早晚还要通过(1)去更新, 这种情况随便搞
存在以las为根的子树中的一条链的长度(不是最长链) == las 到 x + d[y] (d[x] las在y的子树)
d[x] > d[y] + cost(x, y) las 一定在 x 已经遍历过的链上, 那么 cnt = res - dep[las]
d[x] == d[y], cnt = 0,
d[x] < d[y] + cost(x, y) las在以y为根的子树, cnt = cur - dep[las]
再来看 res
- d[y] > d[x], res = cur;
- d[y] == d[x], res = x(不存在公共路径)
然后 dep数组可以dfs省略
做到时间空间都很小
#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
const int N = 2e5 + 5;
int n, m, cnt, las;
vector<pair<int, int>> h[N];
long long d[N], ans;
int dfs(int x, int fa, int dep) {
int res = dep;
for (auto& [y, c] : h[x]) if (y != fa) {
int cur = dfs(y, x, dep + 1);
if (ans < d[x] + d[y] + c)
ans = d[x] + d[y] + c, las = dep, cnt = res + cur - dep * 2;
else if (ans == d[x] + d[y] + c) {
if (d[y] + c >= d[x]) cnt = cur - las;
else cnt = res - las;
}
if (d[x] < d[y] + c) d[x] = d[y] + c, res = cur;
else if (d[x] == d[y] + c) res = dep;
}
return res;
}
int main() {
IOS; cin >> n;
for (int i = 1; i < n; ++i) {
int u, v, c; cin >> u >> v >> c;
h[u].emplace_back(v, c); h[v].emplace_back(u, c);
}
dfs(1, 0, 1); cout << ans << '\n' << cnt;
return 0;
}


折磨牛
好棒!DPyyds
能不能读一遍再发题解啊。
好多地方读都读不通……
还有错字……
效率高,但不好懂…