集合

​ 给定 $n$ 堆石子，以及 $k$ 种操作（集合 $P$）。

​ 有两名玩家轮流操作，每次操作可以从任意一堆石子种拿去石子，但是拿取的数量只能是 $k$ 种操作中的一种，最后无法进行操作的人视为失败。

​ 问如果两人都采用最优策略，先手是否必胜。

​ 首先了解 $SG(x)$ 函数， $x$ 代表局面，$SG(x)$ 代表由局面 $x$ 的局面序数中能够到达的局面中无法到达的最小的局面序数。其中 $SG(x)=0$ 时代表局面 $x$ 是必败的，也就是无法继续合法的操作的局面。（局面序数是个人不严谨的定义，只为更好的理解。）

​ 直观的说，如果 $x$ 能够到达 $0,1,2$，则$SG(x)=3$。如果 $x$ 能够到达 $1,3,4$，那么 $SG(x)=0$，因为 $x$ 无法到达 $0,2,5,6\cdots$，最小的就是 $0$ 。

​ 最后将所有石子堆的 $SG$ 值异或和起来，不为 $0$ 则必胜，反之必败。

​ 画图举例：（以 $n = 2,4,7$ $k = 2,5$ 为例）

​ 首先考虑 7 个石子的一堆，总共能走的局面如下：

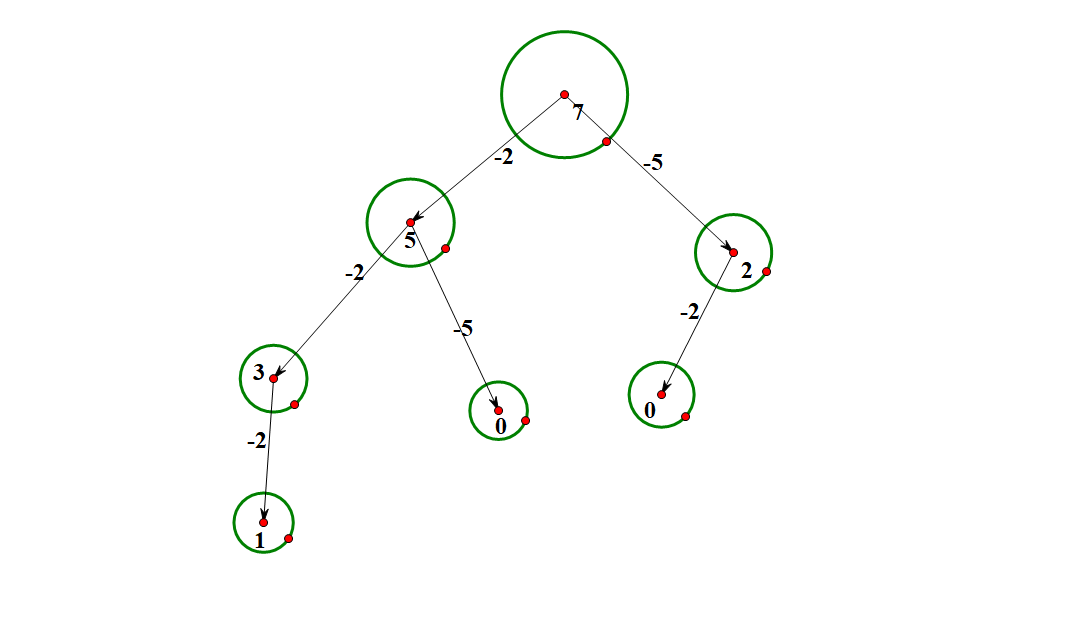
​ 可以看到，所有的叶节点都是无法操作的，也就是 $SG$ 值为 0。$SG(0) = SG(1) = 0$。

​ 再根据 $SG$ 函数的定义，可以推出其他局面的 $SG$ 值。

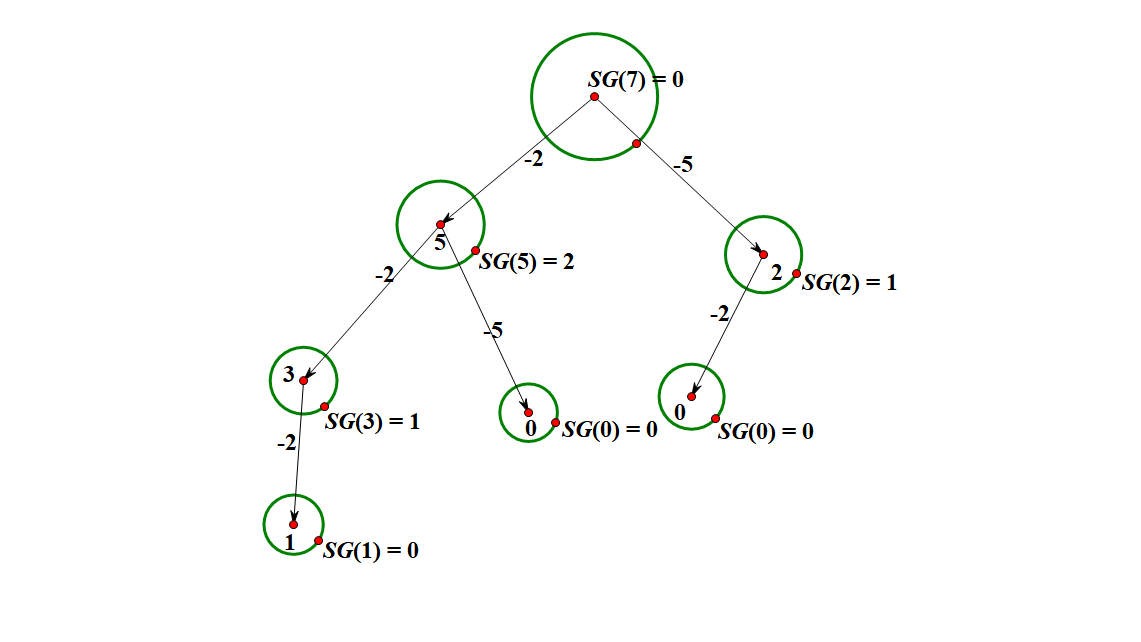
​ 最后将所有石子堆的 $SG$ 值用同样的方法求出来并异或起来得到答案。

注意：本人写的代码只是为了更好的理解和模块化，请尽量自行写出自己熟练的模板和实用的模板（时间短的），或者参考y总的代码风格来写。

代码

typedef vector<int> vi;

int f[N];

int sg(int x, vi P){
    if ( ~ f[x])    return f[x]; //记忆化搜索

    bool vis[N] = {0};
    for (auto it : P){
        if (x >= it)
            vis[sg(x - it, P)] = 1;
    }

    for (int i = 0; ; i ++ )
        if (!vis[i])    return f[x] = i;
}

int solve(vi a, vi P){
    int ans = 0;
    for (auto it : a){
        ans ^= sg(it, P);
    }

    return ans;
}

完整代码

#include <bits/stdc++.h>

using namespace std;

typedef vector<int> vi;

const int N = 1e4 + 10;

int f[N];

int sg(int x, vi P){
    if ( ~ f[x])    return f[x];

    bool vis[N] = {0};
    for (auto it : P)
        if (x >= it)
            vis[sg(x - it, P)] = 1;

    for (int i = 0; ; i ++ )
        if (!vis[i])    return f[x] = i;
}

int solve(vi a, vi P){
    int ans = 0;
    for (auto it : a){
        ans ^= sg(it, P);
    }

    return ans;
}

int main(){
    memset(f, -1, sizeof f);

    int k;
    cin >> k;
    vi p;
    while (k -- ){
        int x;
        cin >> x;
        p.push_back(x);
    }

    int n;
    vi a;
    cin >> n;
    while (n -- ){
        int x;
        cin >> x;
        a.push_back(x);
    }

    cout << (solve(a, p) ? "Yes" : "No");

    return 0;
}

回顾拿石头

对于每一堆石子，数量为$a_i$，那么他能拿走$[1,a_i-1]$，此时能够容易的分析出$SG(a_i)=a_i$。
做法与此题很相似！