$\color{green}{<–画图不易，点下这里赞一下吧}$

思路：

用f[i][j]表示第一个字符串的前 i 个字母变为第二个字符串的前 j 个字母所用的最少操作次数。

假设第一个字符串为：AGTCTGACGC

第二个字符串为：AGTAAGTAGGC

f[3][5] 表示把第一个字符串的前三个字母变为第二个字符串的前五个字母所需要的最少操作次数。

也就是把AGT变为AGTAA所用的最少操作次数。

分析递推方程：

把第一个字符串的前 i 个字母变为第二个字符串的前 j 个字母，有三种方法：

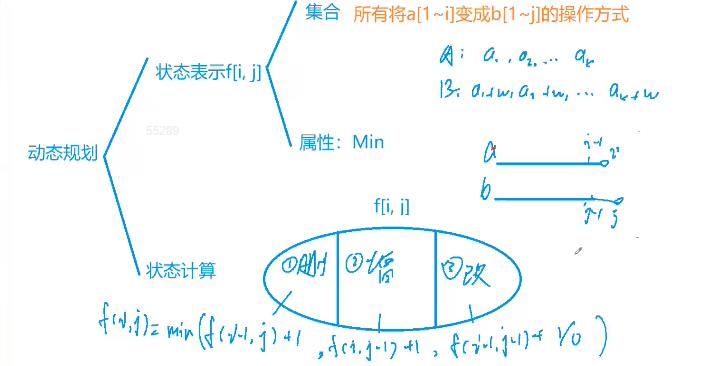
• 把第一个字符串的前 i 个字母变为第二个字符串的前 j - 1 个字符，然后在第一个字符串后面增加第二个字符串的第j个字母。

  这种情况下，f[i][j] = f[i][j - 1] + 1。

  例如：把AGT变为AGTAA，可以先把AGT变为AGTA，然后再在最后面添加一个字符A。

• 把第一个字符串的前 i - 1 个字母变为第二个字符串的前 j 个字符，然后去掉最后一个字符。

  例如：把AGT变为AGTAA，可以先把AGT变为AGTAAT，然后再去掉一个字符T。

  这种情况下，f[i][j] = f[i - 1][j] + 1。

• 把第一个字符串的前 i - 1 个字母变为第二个字符串的前 j - 1个字符。变化之后，对比最后一个字符，如果相等，则变换完成，如果不同，把第一个字符串的最后一个字符变为第二个字符串的最后一个字符，

  例如：把AGT变为AGTAA，可以先把AGT变为AGTAT，然后再在最后面添加一个字符T变为A。

  例如：把AGT变为AGTAT，可以先把AGT变为AGTAT，因为最后一个字符相同，不再做处理。

  这种情况下，f[i][j] = f[i - 1][j - 1] + 1(最一个字符不同) 或f[i][j] = f[i - 1][j + 1] (最一个字符相同)。

取三种情况的最小值，就是f[i][j]。

时间复杂度：O(n^2)。

代码：

#include <iostream>
using namespace std;
const int N = 1010;

char a[N], b[N];//分别存放两个字符串
int f[N][N];//存储结果

int n, m;//两个字符串的长度

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i];

    cin >> m;
    for(int i = 1; i <= m; i++) cin >> b[i];
    //边界，a 字符串的前 i 个字符变为 b 字符串的前 0 个字符，需要 i 步
    for(int i = 0; i <= n; i++) f[i][0] = i;
    //边界，a 字符串的前 0 个字符变为 b 字符串的前 i 个字符，需要 i 步
    for(int i = 0; i <= m; i++) f[0][i] = i;

    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <=m; j++)
        {
            //情况一 二
            f[i][j] = min(f[i][j - 1] + 1, f[i - 1][j] + 1);
            //情况三
            if(a[i] != b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
            else f[i][j] = min(f[i][j], f[i - 1][j - 1]);
        }
    }
    //f[n][m] 表示 a 字符传递额前 n 个字符变为 b 字符传递额前 m 个字符需要的最少步骤。
    cout << f[n][m];
}

有问题直接留言即可，求个点赞~~~