@TOC

剑指 Offer 62. 圆圈中最后剩下的数字

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例 1：

输入: n = 5, m = 3
输出: 3

示例 2：

输入: n = 10, m = 17
输出: 2

限制：

• 1 <= n <= 10^5
• 1 <= m <= 10^6

解题思路

经典的约瑟夫环问题，学过数据结构的同学应该都知道该问题，但那时候是学循环链表的时候引入约瑟夫环问题的，可以直接用现成的循环链表。而这里我们为了解题，特地去构造一个循环链表，显然不太划算，所以考虑其他方法。

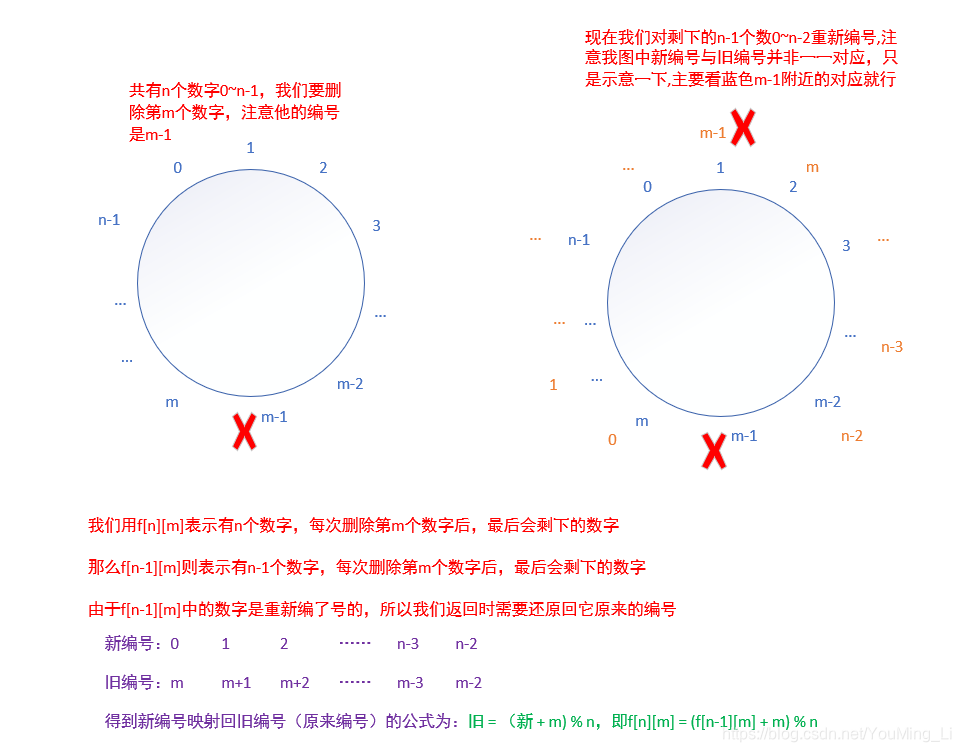
递归方式，如图

Java代码

class Solution {
    public int lastRemaining(int n, int m) {
        if(n == 1) return 0;//如果只剩下一个数字了，递归结束，且该数字在该轮的新编号是0
        return (lastRemaining(n - 1,m) + m) % n;
    }
}