图1.

图2.

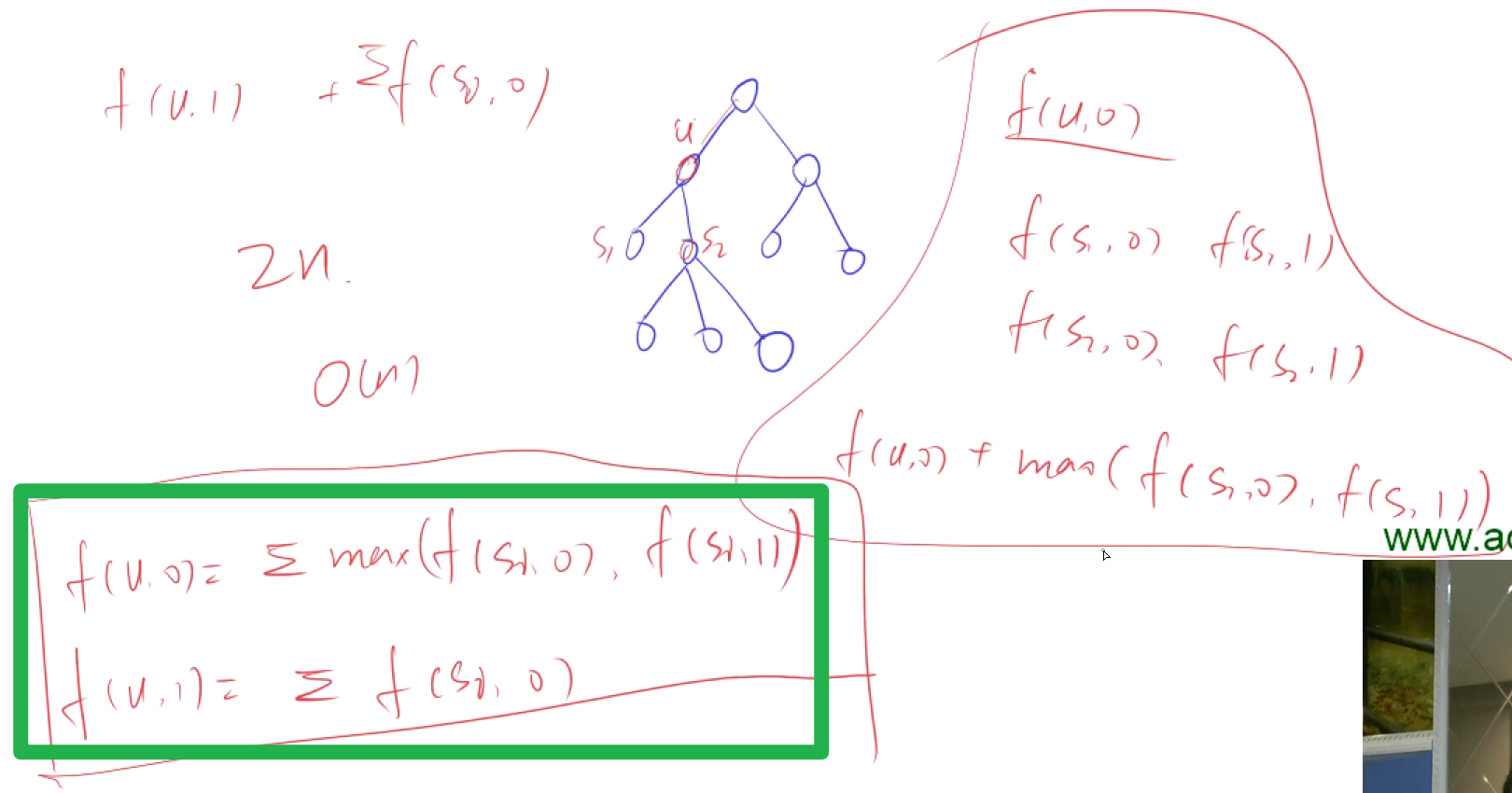
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 6010;
int n;
int happy[N];
int h[N], e[N], ne[N], idx; //树用邻接表来存

int f[N][2];
bool has_father[N];

void add(int a, int b) { // 在a后面插入一条边
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void dfs(int u) { //递归求一下每个状态，从根节点开始
    f[u][1] = happy[u]; //f[u][1]：选择u这个点，令f[u][1] = happy[u] 选它就得加上它的高兴度
    for (int i = h[u]; i != -1; i = ne[i]) { //枚举u的所有儿子
        int j = e[i]; //j表示u的某个儿子
        dfs(j);     //!!!!
        f[u][0] += max(f[j][0], f[j][1]);
        f[u][1] += f[j][0];
    }
}

int main () {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) scanf("%d", &happy[i]);
    memset(h, -1, sizeof h); // 初始化邻接表
    for (int i = 0; i < n - 1; i ++) { //没有说根节点是谁，所以要求一下根节点（没有父亲的节点）
        int a, b;
        scanf("%d%d", &a, &b); // 读入n-1条边  a->b  b是a的父节点
        has_father[a] = true;
        add(b, a);
    }

    int root = 1; //!!!!  //求根节点，从1开始枚举根节点即可 //!!!!
    while (has_father[root])  root ++; //直到没有父节点为止
    dfs(root);
    printf("%d\n", max(f[root][0], f[root][1])); //输出选择根节点的最大值，以及 不选根节点的最大值
    return 0;
}