题目描述
给定一个双向链表,除了下一个和前一个指针之外,它还有一个子指针,可能指向单独的双向链表。这些子列表可能有一个或多个自己的子项,依此类推,生成多级数据结构,如下面的示例所示。
扁平化列表,使所有结点出现在单级双链表中。给定列表第一级的头部。
样例
输入:
1---2---3---4---5---6--NULL
|
7---8---9---10--NULL
|
11--12--NULL
输出:
1-2-3-7-8-11-12-9-10-4-5-6-NULL
样例解释
给出以下多级双向链表:
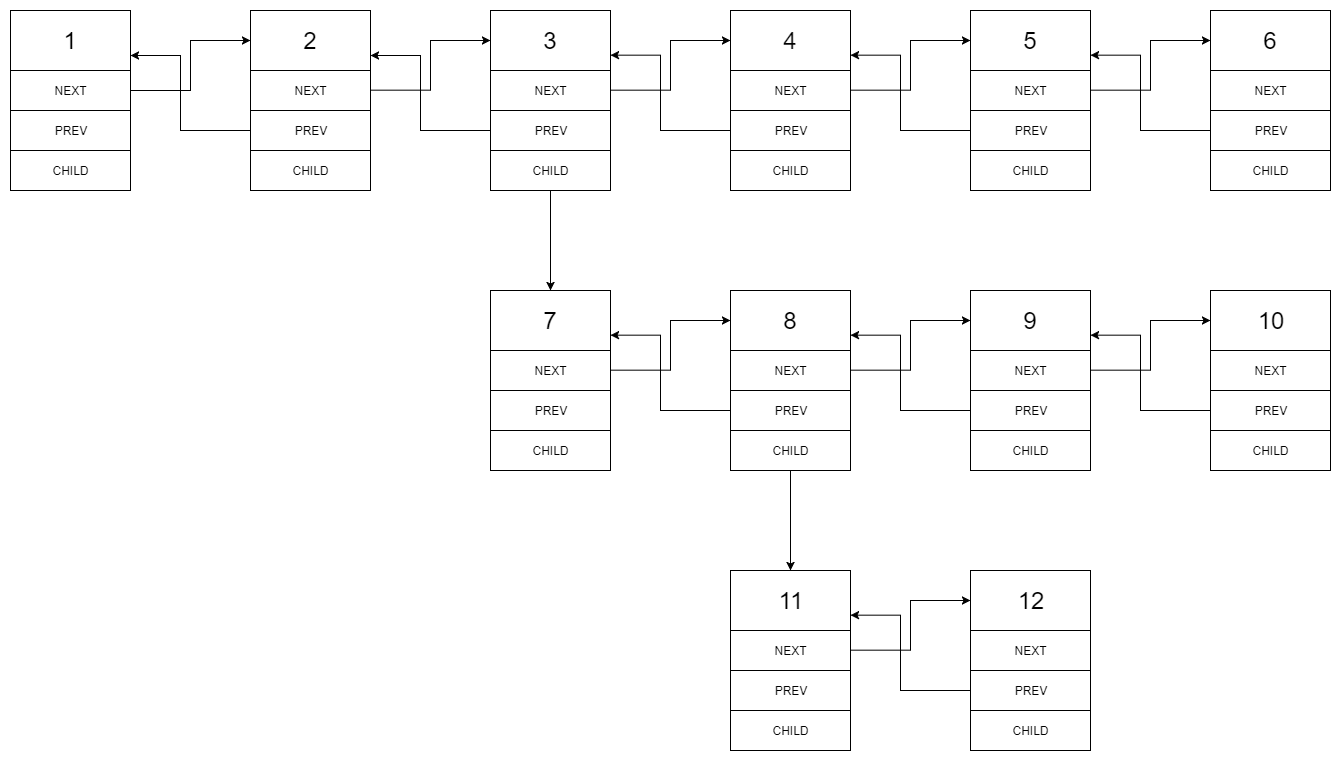
我们应该返回如下所示的扁平双向链表:

算法
(递归) $O(n)$
- 定义
solve函数,参数为当前级链表的头结点,返回当前级链表扁平化后的最后一个结点。 - 在
solve函数中,从头结点开始遍历,如果当前结点cur有child结点:- 则用临时变量
chi和nxt记录下当前结点的child和next,然后递归调用solve(chi),用临时变量tail记录调用的返回值。 - 递归结束后,需要修改当前结点
cur的child和next,以及chi结点的prev。修改tail的next。如果nxt不为空,则修改nxt的prev为tail。 - 最后移动当前结点
cur为nxt。
- 则用临时变量
- 如果当前结点没有
child结点,则直接向后移动当前结点cur。
时间复杂度
- 每个结点仅遍历一次,故时间复杂度为 $O(n)$。
空间复杂度
- 递归需要系统栈空间,故空间复杂度为链表的最大级数。
C++ 代码
/*
// Definition for a Node.
class Node {
public:
int val;
Node* prev;
Node* next;
Node* child;
Node() {}
Node(int _val, Node* _prev, Node* _next, Node* _child) {
val = _val;
prev = _prev;
next = _next;
child = _child;
}
};
*/
class Solution {
public:
Node* solve(Node* head) {
Node *cur = head, *last = NULL;
while (cur) {
if (cur -> child) {
Node *chi = cur -> child;
Node *nxt = cur -> next;
Node *tail = solve(chi);
cur -> child = NULL;
cur -> next = chi;
chi -> prev = cur;
tail -> next = nxt;
if (nxt)
nxt -> prev = tail;
last = tail;
cur = nxt;
} else {
last = cur;
cur = cur -> next;
}
}
return last;
}
Node* flatten(Node* head) {
solve(head);
return head;
}
};

