#include <iostream>
#include <algorithm>

using namespace std;

const int N = 16;
int n;
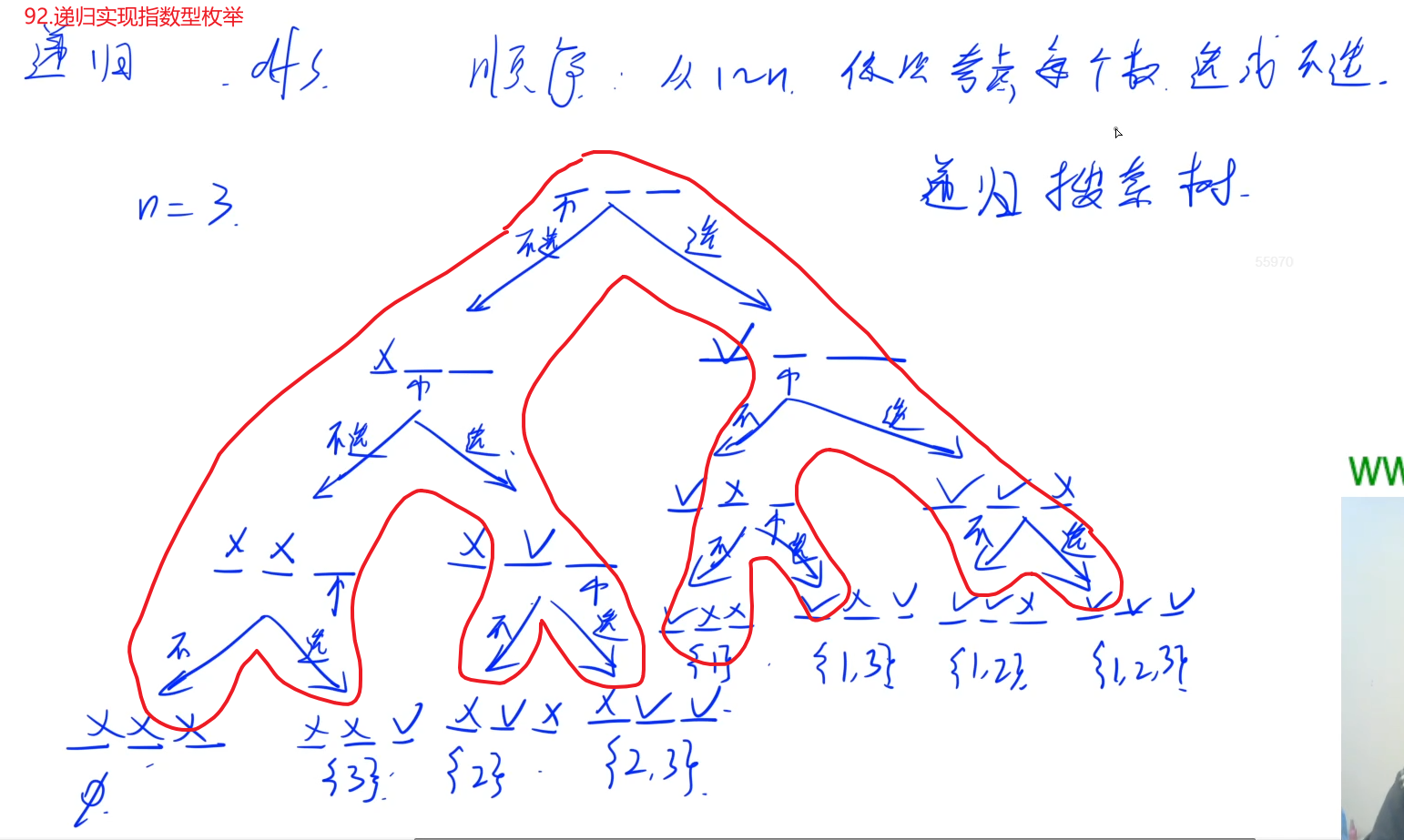
int st[N]; //记录每个位置当前的状态， 0：还没考虑， 1：表示选它， 2：表示不选它

void dfs(int u) {
    if (u > n) {
        for (int i = 1; i <= n; i ++) 
            if (st[i] == 1)
                printf("%d ", i);
        puts("");
        return ; //不能忘
    }

    st[u] = 2; //第一个分支不选
    dfs(u + 1); //进入下一层递归判断当前分支的分支是否选？直到所有左侧分支（不选的）是否判断完（就是是否u>n）如果是就要回溯了，
                //回溯到倒数第二层，将原来状态恢复成st[u] = 0,表示当前位置的分支还没有考虑，下一步就是考虑选它（走右分支）st[u]=1
    st[u] = 0;

    st[u] = 1;
    dfs(u + 1);
    st[u] = 0;
}

int main () {
    cin >> n;
    dfs(1);
    return 0;
}

使用vector[HTML_REMOVED]> ways 的代码：（时间复杂度比普通的慢2倍）

#include <vector>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 16;
int n;
int st[N]; //记录每个位置当前的状态， 0：还没考虑， 1：表示选它， 2：表示不选它
vector<vector<int>> ways;

void dfs(int u) {
    if (u > n) {
        vector<int> way;
        for (int i = 1; i <= n; i ++) 
            if (st[i] == 1)
                // printf("%d ", i);
                way.push_back(i);
        ways.push_back(way);
        // puts("");
        return ;
    }

    st[u] = 2; //第一个分支不选
    dfs(u + 1); //进入下一层递归判断当前分支的分支是否选？直到所有左侧分支（不选的）是否判断完（就是是否u>n）如果是就要回溯了，
                //回溯到倒数第二层，将原来状态恢复成st[u] = 0,表示当前位置的分支还没有考虑，下一步就是考虑选它（走右分支）st[u]=1
    st[u] = 0;

    st[u] = 1;
    dfs(u + 1);
    st[u] = 0;
}

int main () {
    cin >> n;
    dfs(1);

    for (int i = 0; i < ways.size(); i ++) { //这里不能写成i = 1; i <= ways.size()下面同样
        for (int j = 0; j < ways[i].size(); j ++)
            printf("%d ", ways[i][j]);
            puts("");
    }
    return 0;
}