题目描述

给你一个二维整数数组 orders，其中每个 orders[i] = [price_i, amount_i, orderType_i] 表示有 amount_i 笔类型为 orderType_i、价格为 price_i 的订单。

订单类型 orderType_i 可以分为两种：

• 0 表示这是一批采购订单 buy
• 1 表示这是一批销售订单 sell

注意，orders[i] 表示一批共计 amount_i 笔的独立订单，这些订单的价格和类型相同。对于所有有效的 i，由 orders[i] 表示的所有订单提交时间均早于 orders[i+1] 表示的所有订单。

存在由未执行订单组成的 积压订单。积压订单最初是空的。提交订单时，会发生以下情况：

• 如果该订单是一笔采购订单 buy，则可以查看积压订单中价格 最低 的销售订单 sell。如果该销售订单 sell 的价格 低于或等于 当前采购订单 buy 的价格，则匹配并执行这两笔订单，并将销售订单 sell 从积压订单中删除。否则，采购订单 buy 将会添加到积压订单中。
• 反之亦然，如果该订单是一笔销售订单 sell，则可以查看积压订单中价格 最高 的采购订单 buy。如果该采购订单 buy 的价格 高于或等于 当前销售订单 sell 的价格，则匹配并执行这两笔订单，并将采购订单 buy 从积压订单中删除。否则，销售订单 sell 将会添加到积压订单中。

输入所有订单后，返回积压订单中的 订单总数。由于数字可能很大，所以需要返回对 10^9 + 7 取余的结果。

样例

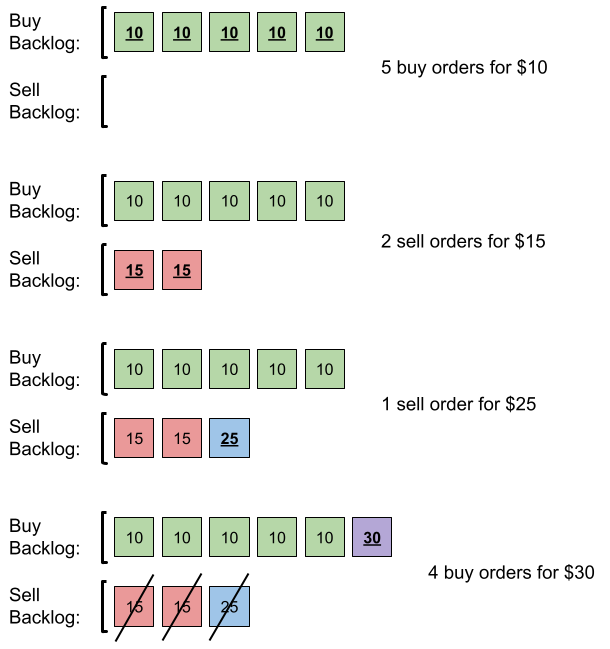
输入：orders = [[10,5,0],[15,2,1],[25,1,1],[30,4,0]]
输出：6
解释：输入订单后会发生下述情况：
- 提交 5 笔采购订单，价格为 10 。没有销售订单，所以这 5 笔订单添加到积压订单中。
- 提交 2 笔销售订单，价格为 15 。没有采购订单的价格大于或等于 15 ，所以这 2 笔订单添加到积压订单中。
- 提交 1 笔销售订单，价格为 25 。没有采购订单的价格大于或等于 25 ，所以这 1 笔订单添加到积压订单中。
- 提交 4 笔采购订单，价格为 30 。前 2 笔采购订单与价格最低（价格为 15）的 2 笔销售订单匹配，从积压订单中删除这 2 笔销售订单。
    第 3 笔采购订单与价格最低的 1 笔销售订单匹配，销售订单价格为 25 ，从积压订单中删除这 1 笔销售订单。
    积压订单中不存在更多销售订单，所以第 4 笔采购订单需要添加到积压订单中。
最终，积压订单中有 5 笔价格为 10 的采购订单，和 1 笔价格为 30 的采购订单。所以积压订单中的订单总数为 6。

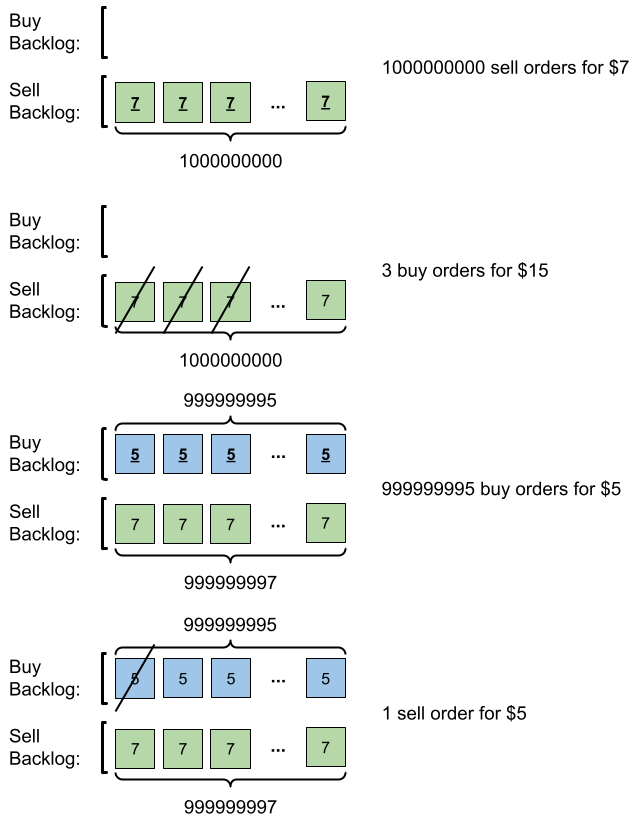
输入：orders = [[7,1000000000,1],[15,3,0],[5,999999995,0],[5,1,1]]
输出：999999984
解释：输入订单后会发生下述情况：
- 提交 109 笔销售订单，价格为 7 。没有采购订单，所以这 109 笔订单添加到积压订单中。
- 提交 3 笔采购订单，价格为 15 。这些采购订单与价格最低（价格为 7 ）的 3 笔销售订单匹配，从积压订单中删除这 3 笔销售订单。
- 提交 999999995 笔采购订单，价格为 5 。销售订单的最低价为 7 ，所以这 999999995 笔订单添加到积压订单中。
- 提交 1 笔销售订单，价格为 5 。这笔销售订单与价格最高（价格为 5 ）的 1 笔采购订单匹配，从积压订单中删除这 1 笔采购订单。
最终，积压订单中有 (1000000000-3) 笔价格为 7 的销售订单，和 (999999995-1) 笔价格为 5 的采购订单。
    所以积压订单中的订单总数为 1999999991 ，等于 999999984 % (10^9 + 7)。

限制

• 1 <= orders.length <= 10^5
• orders[i].length == 3
• 1 <= price_i, amount_i <= 10^9
• orderType_i 为 0 或 1。

算法

(堆) $O(n \log n)$

1. 使用大根堆维护当前积压的买单，使用小跟堆维护当前积压的卖单。
2. 新的买单来到时，从卖单堆中弹出栈顶去匹配当前的买单。如果不符合要求，或者已经匹配完成，则结束。
3. 同理，新的卖单来到时，从买单堆中弹出栈顶去匹配当前的卖单。
4. 最后，统计两个堆中剩余的订单数量。

时间复杂度

• 总的来看，每笔订单最多进堆一次，出堆一次，故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储两个堆。

C++ 代码

struct Buy {
    int price, amount;

    Buy(int price_, int amount_):price(price_), amount(amount_){}

    bool operator < (const Buy &another) const {
        return price < another.price;
    }
};

struct Sell {
    int price, amount;

    Sell(int price_, int amount_):price(price_), amount(amount_){}

    bool operator < (const Sell &another) const {
        return price > another.price;
    }
};

class Solution {
public:
    int getNumberOfBacklogOrders(vector<vector<int>>& orders) {
        priority_queue<Buy> b;
        priority_queue<Sell> s;

        for (const auto &o : orders) {
            int price = o[0], amount = o[1];
            if (o[2] == 0) {
                while (amount > 0 && !s.empty()) {
                    Sell top = s.top();
                    if (top.price > price) break;
                    s.pop();

                    if (top.amount > amount) {
                        top.amount -= amount;
                        amount = 0;
                        s.push(Sell(top.price, top.amount));
                    } else {
                        amount -= top.amount;
                    }
                }
                if (amount > 0)
                    b.push(Buy(price, amount));
            } else {
                while (amount > 0 && !b.empty()) {
                    Buy top = b.top();
                    if (top.price < price) break;
                    b.pop();

                    if (top.amount > amount) {
                        top.amount -= amount;
                        amount = 0;
                        b.push(Buy(top.price, top.amount));
                    } else {
                        amount -= top.amount;
                    }
                }
                if (amount > 0)
                    s.push(Sell(price, amount));
            }
        }

        const int mod = 1000000007;
        int ans = 0;
        while (!s.empty()) {
            ans = (ans + s.top().amount) % mod;
            s.pop();
        }

        while (!b.empty()) {
            ans = (ans + b.top().amount) % mod;
            b.pop();
        }

        return ans;
    }
};