算法一：暴力枚举

算法思路

1、通过观察可以发现，我们每一个数都必须回到它自己的位置上，比如 1 必须在第一位，2 必须在第二位上

2、那么我们就可以这样操作，由于每个数必须回到自己的位置，直接从 1 枚举到 $n$ ，如果当前位置的数不等于它的下标，那么我们就必须要把它给替换掉

3、设当前位置为 $i$ 的话，那么我们就从 $i+1$ 开始往后枚举，直到找到对应的 a[$j$] 和我们的 $i$ 相等，那么我们就把上个数交换，把交换次数++

4、容易证明这个算法的正确性，由于每个数必须回到原来的位置，所以我们这样子操作不会出现多于的步骤，因为每次操作都是必须的，即使这个算法看起来很麻烦

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>

using namespace std;

const int N=10010;

int n;

int a[N];

int main()
{
    scanf("%d",&n);

    for(int i=1;i<=n;i++)scanf("%d",&a[i]);

    int sum=0;
    for(int i=1;i<=n;i++)
    {
        if(a[i]!=i)//直接遍历，如果不是自身的话，我们必然要交换，所以不会出现多于的操作
        {
            for(int j=i+1;j<=n;j++)
            if(a[j]==i)
             swap(a[i],a[j]);

             sum++;
        }
    }

    printf("%d\n",sum);

    return 0;
}

算法二：置换群算法

算法思路

1、由$y$总分析可知，如果我们当前位置的 $i$$\neq$a[$i$]的话，那么它必然等于其他位置上的 a[$i$]

2、那么我们可以利用图的存储方式来描述我们整个数组

3、下面借用一下y总上课画的图

4、我们连接的方式是把我们当前的位置的 a[$i$]连向我们本该在的位置的 a[$i$]，（也可以理解为每 个$i$ 都连向它的a[$i$]，乱序的时候）那按这个规则连起来的话就会得到以上的联系规则

5、不难证明，如果把一个题目中所述的序列按照上述方法连接后，每一个连接都会是一个环，要么是自环，要么是与别人成环（因为总是会连回来的，因为每个位置的出度一定为 1 ，入度也一定为 1 ，所以必然成环 出度是指它所连向的点的数量，入度是指连向它的点的数量）

6、那么通过进一步分析可以知道，一个长度为 $n$ 的序列做多会存在 $n$ 个环，那就是当该序列为升序排列时，也就是题中所述的目标状态时

7、那么我们如果去操作这个方法呢？

8、其实我们不需要像的和图论题一样去真的去构造那么多环，我们只是利用这个思想，来模拟这个过程

9、下面讲一下具体的操作，引用一下$y$总上课画的图

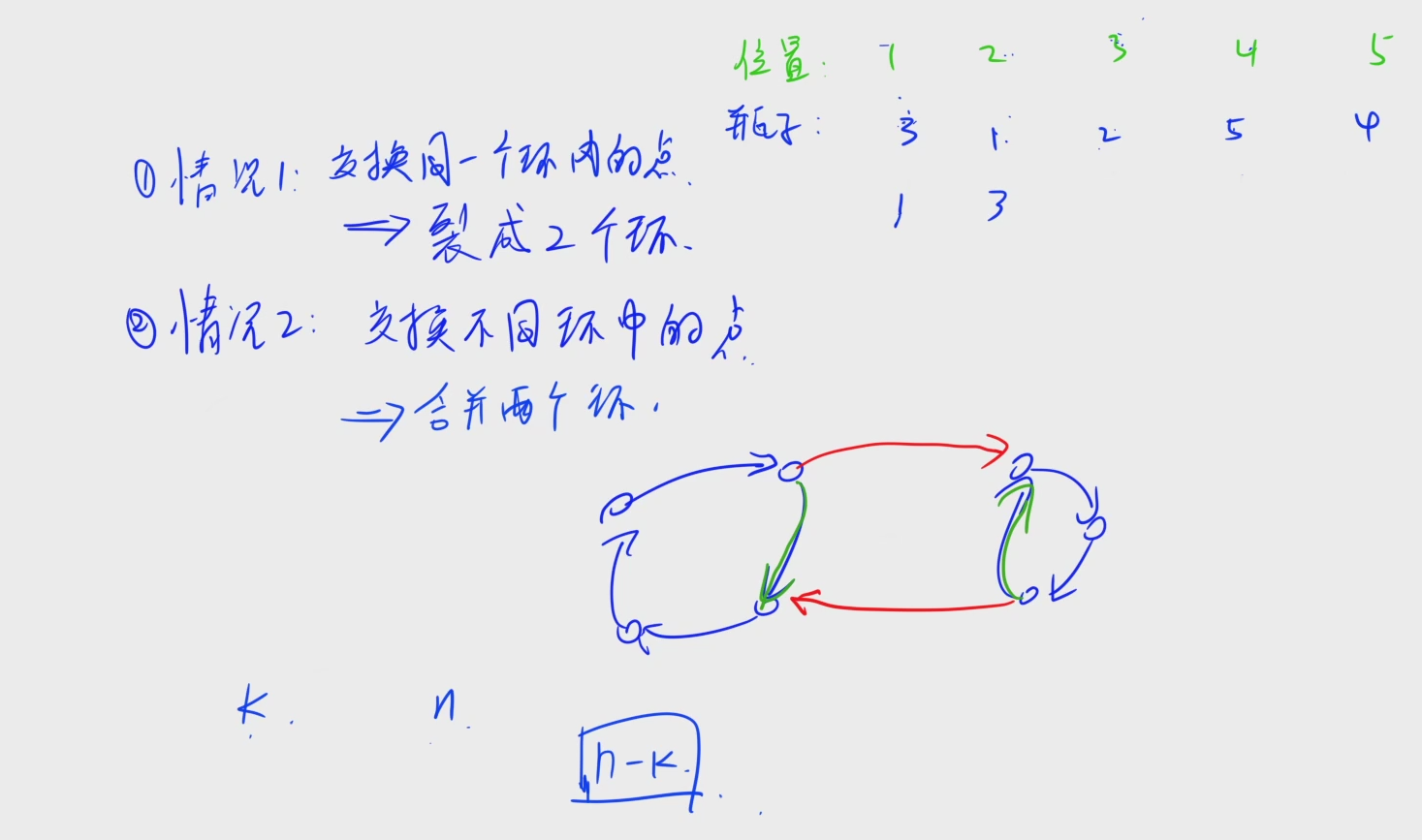
10、我们对于每一个环的操作，最多有两种情况，如上图所示，我们要么是在环内操作，要么就是跨环操作（环内操作就是在环内切换连接对象，环外操作就是在环与环之间切换连接对象）

11、其实上面的操作全都是一种思想，目的是为了引出一个结论，假设我们当前有 $k$ 个环，但是我们最终情况是我们需要有 $n$ 个环，所以我们至少需要操作 $n-k$ 次（$k$显然小于$n$哈）

12、上面的所有描述都是为了证明，我们确实可以取到我们操作次数的最小值

13、那么我们有了这个结论那我们就可以……

14、等等，你是不是想骗大家，想糊过去是吧，你还没具体讲证明呢？具体操作呢？？$what?$

15、好吧，其实我也不知道为什么这个是成立的，如果按 $y$ 总所说的，只需要操作 $n-k$ 次的话，那就意味着我们每次只能操作环内的情况，只能将一个环一分为二，每次操作必须增加一个环。

16、我怎么感觉也不太对呢……

17、可能是我没有仔细思考啊，我这里也是刚听完课所以把 $y$ 总说的回顾了一遍，等我想通了我再来更新$hh$

18、讲一下代码具体怎么写，这个代码的时间复杂度是 $O(n)$ 的，所以我们采取的方式还是从 1 枚举到 $n$

19、但是不同的是，我们为了保证我们只会把每个数枚举一遍，我们加了一个判重数组，来记录一下这个数是否被用过

20、我们在实际操作的时候呢，其实可以理解为一个“毁环的过程”，如果毁环呢？我们就把我们当前环内的点全部标记一下，那就相当于我们环内的点我们都用过了，不会再重复遍历，对于实际来说这个环就相当于与消失了。

21、我们每消灭一个环，我们就把计数器++，目的是为了记录一下我们一共有多少个环

22、最后利用我们的结论，我们用 $n-k$ 那就是我们要的答案了

23、为什么我现在不把这个想清楚呢？是因为我马上要去上课了，等回来再补充

24、重点是：环其实不需要真实构造，我们可以利用代码简单的实现，这个会在代码里面注释，重要的是我们推出来的结论

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>

using namespace std;

const int N=10010;

int st[N];//判重数组

int a[N];

int n;

int main()
{
    scanf("%d",&n);

    for(int i=1;i<=n;i++)scanf("%d",&a[i]);


    int cnt=0;

    for(int i=1;i<=n;i++)
      if(!st[i])
      {
          cnt++;

          int t=i;

           st[t]=1;

          while(a[t]!=t&&a[t]!=i)//这里就是判断那个环了，先一直往下搜，搜到自己那就是完成了一个环了
          {
              t=a[t];

              st[t]=1;
          }
      }

      printf("%d",n-cnt);//重要的事情说三遍，重要的是结论！！！

      return 0;
}