题目思路:

这是一道非典型的单调栈问题，思路确实很巧妙，记录一下:

1.首先对于i<j<k,求a[i]<a[k]<a[j]是否存在，我们不妨考虑一下简化版的: 求是否存在i<k,

满足a[i]<a[k],这比较容易，从n-1到0线性扫描一遍，r维护i-1到n-1的最大值，对于当前的i，如果a[i]<r, 存在;

2.这道题在a[i]和a[k]之间加入一个a[j],并且要求a[j]>a[k],这样用上面的思路维护i-1到

n-1的时候必须要求a[k]的左边必须存在一个比a[j]>a[k];

3.用栈来考虑这个问题,tmp 维护所有的a[k]的最大值(这里的a[k]必须满足左边存在a[j]>a[k]),这道题的巧妙之处就是用栈来维护tmp:

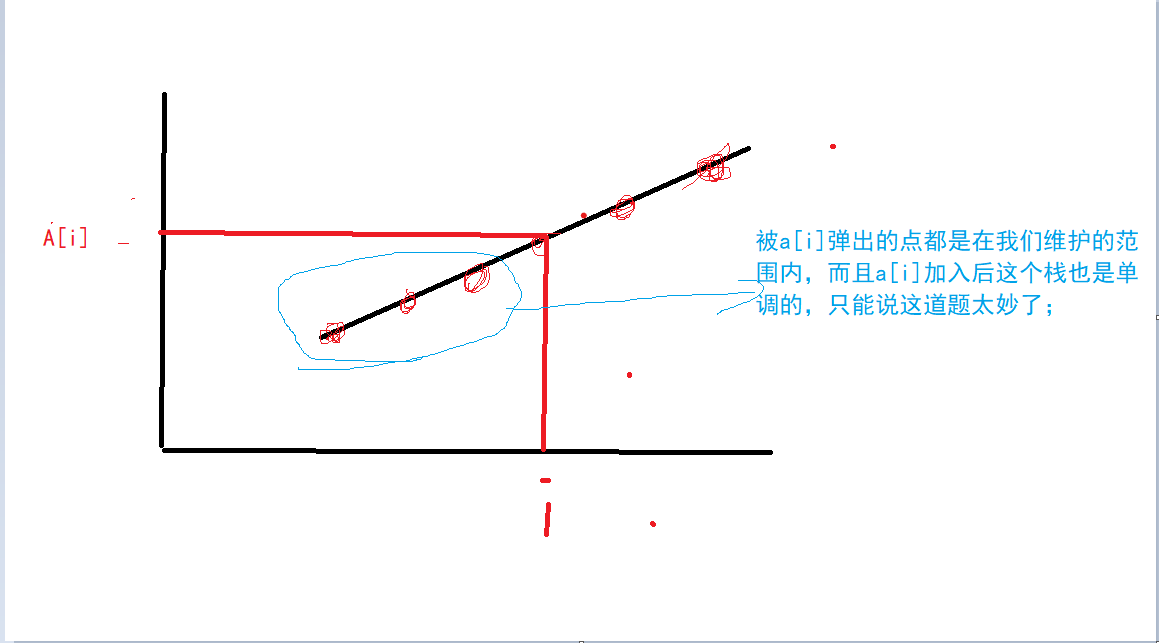
4.从n-1到0扫描一遍，当我们维护的栈是单调递增的时候，当a[i]>stk.top()的时候，我们不断出栈直至a[i]<=stk.top(),这样发现之前出栈的都是小于a[i]的，正好满足我们维护的a[k],即左边存在a[j]>a[k]，用弹出的数来更新最新tmp,所以对于a[i]< tmp 则true;

AC代码

class Solution {
public:
    bool find132pattern(vector<int>& nums) {
    int n=nums.size();
    int tmp=INT_MIN;
    stack<int> stk;
    for(int i=n-1;i>=0;i--){
     if(nums[i]<tmp) return true;
     while(stk.size()&&stk.top()< nums[i]){
         tmp=max(tmp,stk.top());
         stk.pop();
     }
     stk.push(nums[i]);
    }
    return false;
    }
};