P184(基础班笔记)
题解：关于字典树的四道题

我写的Trie树模板
yxc给的两个版本的代码 中 res的两种写法的含义

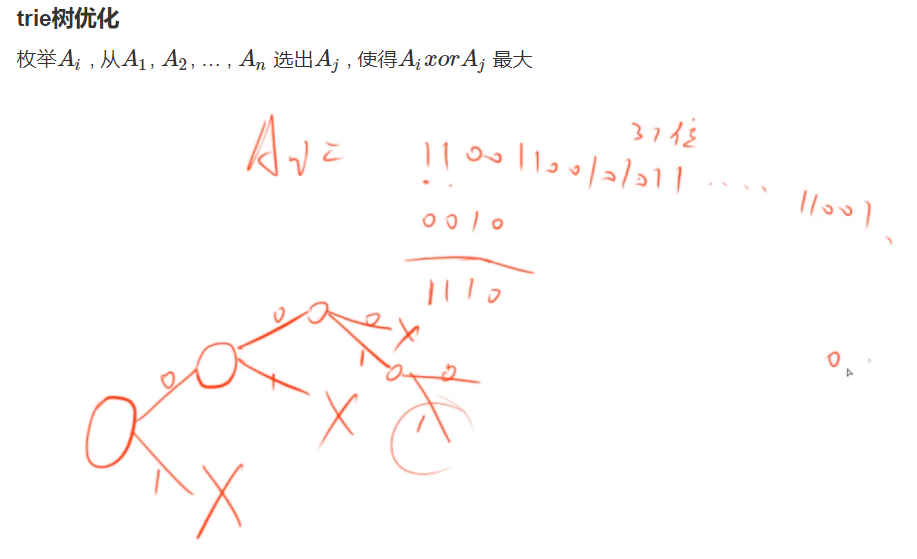
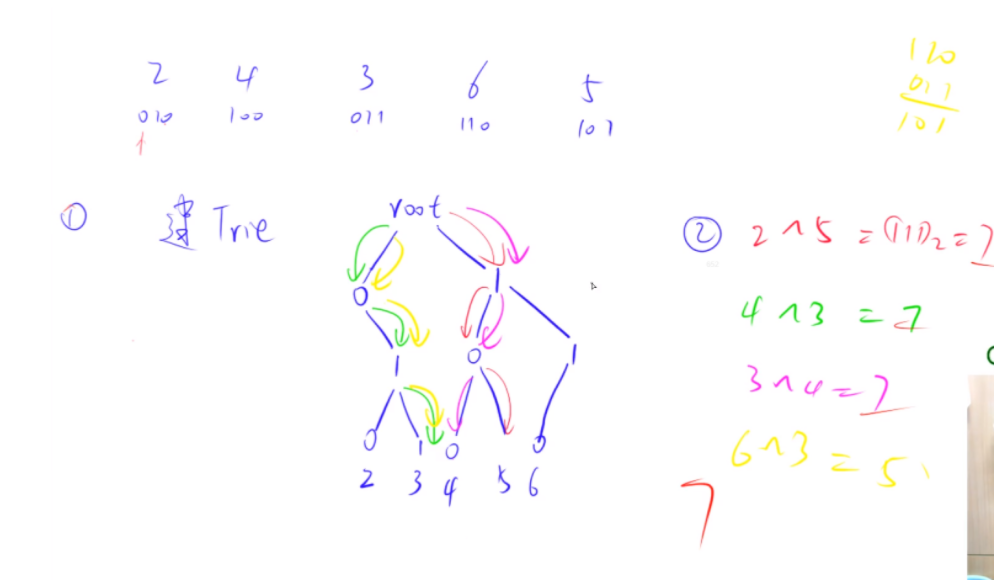
算法模板

int son[N][26], cnt[N], idx;
char str[N];

// p 下标是p的点， p点的所有儿子都存在了son[p]中，
// son[p][0] son[p][1] 分别表示p的第一个儿子，第二个儿子…
// cnt[x]以x结尾的单词数量有多少个

// 插入一个字符串
void insert(char str[]) {
    int p = 0; 
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u])  son[p][u] = ++idx;  
        p = son[p][u];
    }
    cnt[p]++; 
}

//查询字符串出现的次数
int query(char* str) {
    int p = 0; 
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u])  return 0; 
        p = son[p][u];
    }
    return cnt[p]; 
}

本题完整代码

#include <iostream>

using namespace std;

const int N = 1e5 + 10;
const int M = 30 * N;
int son[M][2], idx; // 先定义Trie树 idx是当前已经用到了哪个下标
int a[N];

void insert(int x) {
    int p = 0;
    for (int i = 30; ~i; i --) { // ~i ==> i>=0
        int &s = son[p][x >> i & 1]; // x >> i & 1，x的二进制表示中第i位是0还是1。加&s：s的值需要修改，加上&后s的值改变时，son[][]的值也会改变
        if (!s) s = ++ idx; // 用s来看p的儿子是否存在（有儿子则走0或1，无儿子则建节点++ idx） s = ++ idx;创建新的节点
        p = s; // 不管是否有儿子还是新建的儿子都要让p走到下一个点的位置
    }
    // for循环也可以不用int &s (下面这样写与模板更像)
    /*
        for (int i = 30; ~i; i --) {
        if (!son[p][x >> i & 1])
            son[p][x >> i & 1] = ++ idx;
        p = son[p][x >> i & 1];
    }
    */
}

int query(int x) { //找到和x异或值最大的结果值
    int p = 0, res = 0; // p是在Trie树中遍历的指针
    for (int i = 30; ~i; i --) {
        int s = x >> i & 1;
        if (son[p][!s]) {//先来看一下与x的第i位值不相同的位置是否存在 son[p][!s]
            res += 1 << i; // 值不同的位置存在，则异或后要对最终结果做贡献，res+=2^i
            p = son[p][!s]; //值不同的位置存在,则p一定要走到存在的分支上（就是与x第i位不同的分支上）
        } else {
            p = son[p][s]; //否则(值不同的位置不存在)只能往相同的分支走p = son[p][s];并且不用贡献res了，因为异或结果是0,0^i==0
        }
    }
    return res;
}

int main () {
    int n;
    cin >> n;
    for (int i = 0; i < n; i ++) {
        cin >> a[i];
        insert(a[i]); // 先建Tire树
    }
    int res = 0;
    for (int i = 0; i < n; i ++) {
        res = max(res, query(a[i])); // query(a[i])找到和a[i]异或值最大的结果值（返回的是异或后的结果）
    }
    cout << res << endl;
    return 0;
}