算法

(数学) $O(1)$

可以先对 $n$ 边形作一个外接圆

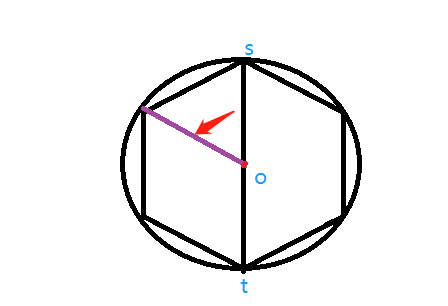
如图所示，待求点的坐标是由 向量 $\vec{os}$ 逆时针旋转 $\frac{2\pi}{n}$ 的弧度得到。
可以借助复数乘法的几何意义来实现：
记 $z_1 = r_1e^{i\theta_1}, z_2 = r_2e^{i\theta_2}$，那么 $z1 \times z2$ 其实就是 $z1$ 绕逆时针旋转一个角 $\theta_2$，再把模长变为原来的 $r_2$ 倍。而本题在逆时针旋转过后不需要改变模长。

C++ 代码

#include <bits/stdc++.h>

using std::cin;
using std::cout;

using C = std::complex<double>;
C inC() {
    double x, y;
    cin >> x >> y;
    return C(x, y);
}

int main() {
    int n;
    cin >> n;

    C s = inC();
    C t = inC();

    C o = (s + t) / 2.0;
    double PI = acos(-1);
    double rad = 2 * PI / n;
    C r(cos(rad), sin(rad));

    C ans = o + (s - o) * r;
    printf("%.10f %.10f\n", ans.real(), ans.imag());

    return 0;
}