题目描述

输入正整数 X，求 X 的大于 1 的因子组成的满足任意前一项都能整除后一项的严格递增序列的最大长度，以及满足最大长度的序列的个数。

输入格式
输入包含多组数据，每组数据占一行，包含一个正整数表示 X。

输出格式
对于每组数据，输出序列的最大长度以及满足最大长度的序列的个数。

每个结果占一行。
数据范围

1≤X≤2的20次方

样例

输入样例：

2
3
4
10
100

输出样例：

1 1
1 1
2 1
2 2
4 6

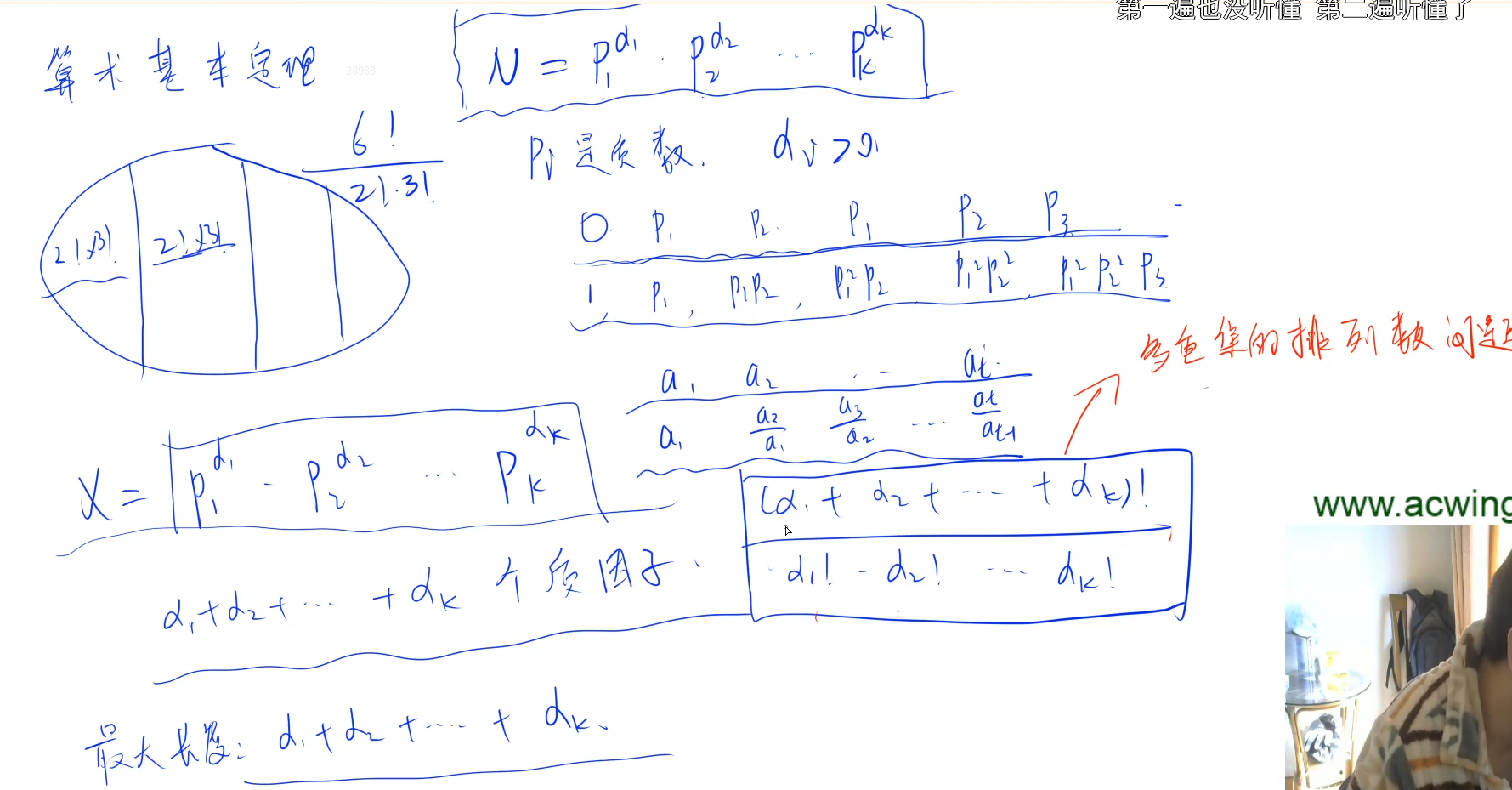
关于多重集组合数

可以理解为是高中数学排列组合的一个应用，应用场合是在排列是去除重复相同项排列的情况
公式为 n!(总排列的数目)/n1!n2!n3!....(每种组合内部的排列数)
为什么要预处理阶乘？

注意到该题最后是要算关于X的因子链序列的最大长度和个数

而关于X的因子链序列的计算便涉及到排列 这是因为不同因子交换顺序便会获得不同的序列
而在此过程中便会产生相同因子的排列情况 通过预处理阶乘便可快速获得阶乘数 
从而不需要在进行多余计算

线性筛选法，O(n)
模板：

void get_prime(){
    for(int i=2;i<=N;i++){
        if(!num[i]){
            primenum[cnt++]=i;
            minp[i]=i;//记录一个数的最小质因数 
        }
        for(int j=0;j<cnt&&primenum[j]*i<=N;j++){
            num[primenum[j]*i]=true;//筛掉的一定是合数，且一定是用最小质因子筛的
            minp[primenum[j]*i]=primenum[j];//记录一个数的最小质因数
            if(i%primenum[j]==0) break;
    } 
    }   
}

#include <iostream> 
#include <algorithm>
using namespace std;
int n;
const int N=(1<<20)+10;
int primenum[N];//把素数存起来 
bool num[N];//判断这个数是否是合数 
int cnt;
int minp[N];//记录一个数的最小质因数 
int sum[N];
long long f[30];
void get_prime(){
    for(int i=2;i<=N;i++){
        if(!num[i]){
            primenum[cnt++]=i;
            minp[i]=i;//记录一个数的最小质因数 
        }
        for(int j=0;j<cnt&&primenum[j]*i<=N;j++){
            num[primenum[j]*i]=true;//筛掉的一定是合数，且一定是用最小质因子筛的
            minp[primenum[j]*i]=primenum[j];//记录一个数的最小质因数
            if(i%primenum[j]==0) break;
    } 
    }   
}

int main(){
    f[0]=1;
      for(int i=1;i<=20;i++)
          f[i]=f[i-1]*i;
          //为啥只有20个因子呢

因为数据最大是2^20，而这个数最小质因子是2，这个数就等于20个2相乘。因此就是最多20个因子。
    int x;
    int fact[30];
    int k;
    int tot;
    long long sum=1;
    get_prime();
    while(scanf("%d",&x)!=EOF){
        tot=0;//因子总个数
        sum=1;
        while(x>1){
            int p=minp[x];
            k=0;//因子出现的次数
            while(x%p==0){
            x/=p;
            k++;
            tot++;  
            }
        sum*=f[k];
        }
        printf("%d %lld\n", tot, f[tot]/sum);
    }


    return 0;
}

#include <iostream> 
#include <algorithm>
using namespace std;
int n;
const int N=(1<<20)+10;
int primenum[N];//把素数存起来 
bool num[N];//判断这个数是否是合数 
int cnt;
int minp[N];//记录一个数的最小质因数 
int sum[N];
void get_prime(int n){
    for(int i=2;i<=n;i++){
        if(!num[i]){
            primenum[cnt++]=i;
            minp[i]=i;
        }
        for(int j=0;j<cnt&&primenum[j]*i<=n;j++){
            num[primenum[j]*i]=true;
            minp[primenum[j]*i]=primenum[j];
            if(i%primenum[j]==0) break;
                //如果i是前面某个素数的倍数时, 说明i以后会由某个更大的数乘这个小素数筛去
                //同理, 之后的筛数也是没有必要的, 因此在这个时候, 就可以跳出循环了
    } 
    }   
}

int main(){
    int x;
    int fact[30];
    int k;
    int tot;
    get_prime(N-1);
    while(scanf("%d",&x)!=EOF){
        k=0;tot=0;
        while(x>1){
            int p=minp[x];
            fact[k]=p;//第k个因子是fact[k]
            sum[k]=0;//第k个因子出现过的次数
            while(x%p==0){
            x/=p;
            sum[k]++;
            tot++;  //因子的总个数
            }
            k++;
        }
        long long res = 1;
        for (int i = 1; i <= tot; i ++ ) res *= i;//因子总个数的阶乘, 求所有质因子出现总次数的全排列
        //去除各个质因子重复出现的次数
        for (int i = 0; i < k; i ++ )
            for (int j = 1; j <= sum[i]; j ++ )
                res /= j;

        printf("%d %lld\n", tot, res);
    }


    return 0;
}

#include <iostream> 
#include <algorithm>
using namespace std;
int n;
const int N=(1<<20)+10;
int primenum[N];//把素数存起来 
bool num[N];//判断这个数是否是合数 
int cnt;
int minp[N];//记录一个数的最小质因数 
int sum[N];
void get_prime(int n){
    for(int i=2;i<=n;i++){
        if(!num[i]){
            primenum[cnt++]=i;
            minp[i]=i;
        }
        for(int j=0;j<cnt&&primenum[j]*i<=n;j++){
            num[primenum[j]*i]=true;
            minp[primenum[j]*i]=primenum[j];
            if(i%primenum[j]==0) break;
    } 
    }   
}

int main(){
    int x;
    int fact[30];
    int k;
    int tot;
    get_prime(N-1);
    while(scanf("%d",&x)!=EOF){
        k=0;tot=0;
        while(x>1){
            int p=minp[x];
            fact[k]=p;
            sum[k]=0;
            while(x%p==0){
            x/=p;
            sum[k]++;
            tot++;  
            }
            k++;
        }
        long long res[tot+5] = {1};
        for (int i = 1; i <= tot; i ++ ) res[i] = i * res[i-1];
        long long s=res[tot];
        for (int i = 0; i < k; i ++ ){
             s/=res[sum[i]];
        }
        printf("%d %lld\n", tot, s);
    }


    return 0;
}