题目描述

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

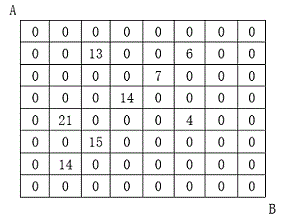
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 1 开始。

一行“0 0 0”表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

N≤10

样例

输入样例:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例:
67

算法1(未优化版)

(动态规划) $O(n^4)$

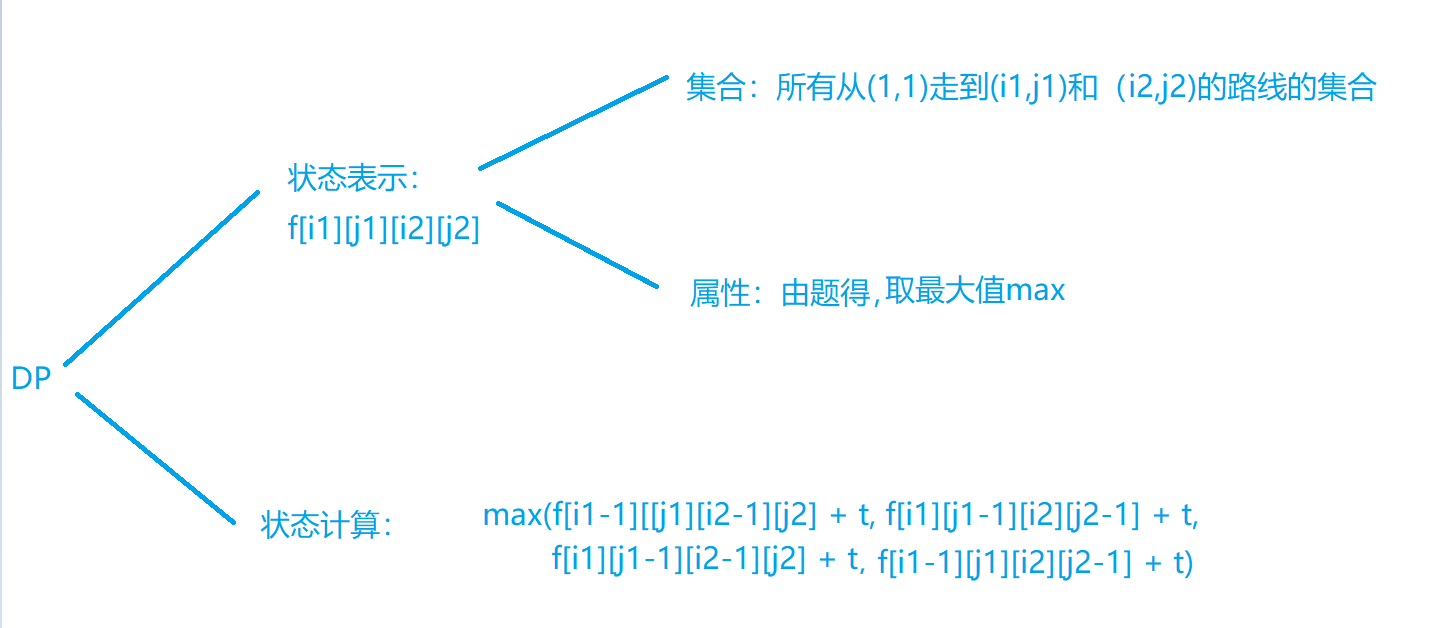
图片里面的t为当前方格的数值(如果两个方格不冲突，则取两个方格的数值，如果重复，只取一次)

状态表示：f[i1][j1][i2][j2]
属性：max

状态计算：
f[i1][j1][i2][j2] = max(f[i1-1][j1][i2-1][j2] + t,f[i1-1][j1][i2][j2-1] + t,
f[i1][j1-1][i2-1][j2] + t, f[i1][j1-1][i2][j2-1] + t)

状态计算解释：
两条路线所在当前方格的最大值可以由上面一格或者左边一格计算出来
，所以两条路线的值的组合一共有四种情况，即 上上，左左，左上， 上左；
最后再加上当前方格的数值(路线方格重合只取一次）

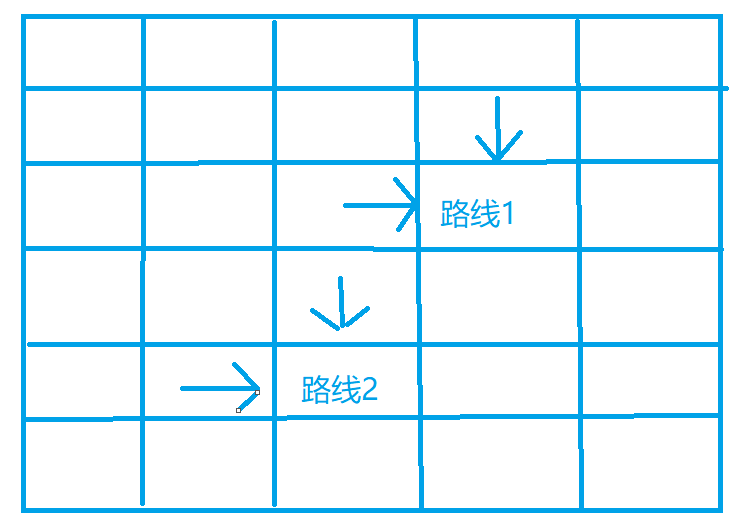
因为f[i1][j1][i2][j2]放的都是从所有路线中数值的最大值，所以可以计算往下或者往右一格的最大值

C++ 代码

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 15;
int n;
int w[N][N];
int f[N][N][N][N];

int main(){
    scanf("%d", &n);
    int a, b, c;
    //输入
    while(cin >> a >> b >> c, a || b || c){
        w[a][b] = c;
    }

    for(int i1 = 1; i1 <= n; i1 ++)
        for(int j1 = 1; j1 <= n; j1++)
            for(int i2 = 1; i2 <= n; i2++)
                for(int j2 = 1; j2 <= n; j2++){
                    int t = w[i1][j1];
                    //如果没有走到同一格，再加上第二个格子的数值
                    if(i1 != i2 || j1 != j2)t += w[i2][j2];
                    int &x = f[i1][j1][i2][j2];
                    x = max(x, f[i1-1][j1][i2-1][j2] + t);
                    x = max(x, f[i1][j1-1][i2][j2-1] + t);
                    x = max(x, f[i1-1][j1][i2][j2-1] + t);
                    x = max(x, f[i1][j1-1][i2-1][j2] + t);
                }

    printf("%d\n", f[n][n][n][n]);
    return 0;
}

算法2(优化版)

(动态规划) $O(n^3)$

由题可知，两条路线每次都走一格
所以坐标和 i1 + j1 = i2 + j2, 然后我们取一个变量 k = i1 + j1 = i2 + j2;
算法1里面有4层循环 j1 和 j2各使用了一个循环
但是有了k之后我们可以用 k 和 i1, i2 计算出 j1, j2 (j1 = k - i1, j2 = k - i2)
这样的话就只需要三层循环

状态表示:f[k][i1][i2] 所有从(1,1)走到 (i1, k-i1), (i2, k-i2)的所有路线的集合
属性：max

C++ 代码

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 15;
int n;
int w[N][N];
int f[N*2][N][N];

int main(){
    scanf("%d", &n);
    int a, b, c;
    while(cin >> a >> b >> c, a || b || c){
        w[a][b] = c;
    }

    for(int k = 2; k <= n * 2; k ++)
        for(int i1 = 1; i1 <= n; i1++)
            for(int i2 = 1; i2 <= n; i2++){
                if(k - i1 >= 1 && k - i1 <= n && k - i2 >= 1 && k - i2 <= n)
                {
                    int t = w[i1][k-i1];
                    if(i1 != i2)t += w[i2][k-i2];
                    int &x = f[k][i1][i2];
                    x = max(x, f[k-1][i1-1][i2-1] + t);
                    x = max(x, f[k-1][i1-1][i2] + t);
                    x = max(x, f[k-1][i1][i2-1] + t);
                    x = max(x, f[k-1][i1][i2] + t);
                }
            }

    printf("%d\n", f[n * 2][n][n]);
    return 0;
}