题目描述

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2)

表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n行，每行包含 m个整数，表示整数矩阵。

接下来 q行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n行，每行 m个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

样例

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

二维矩阵：

二维
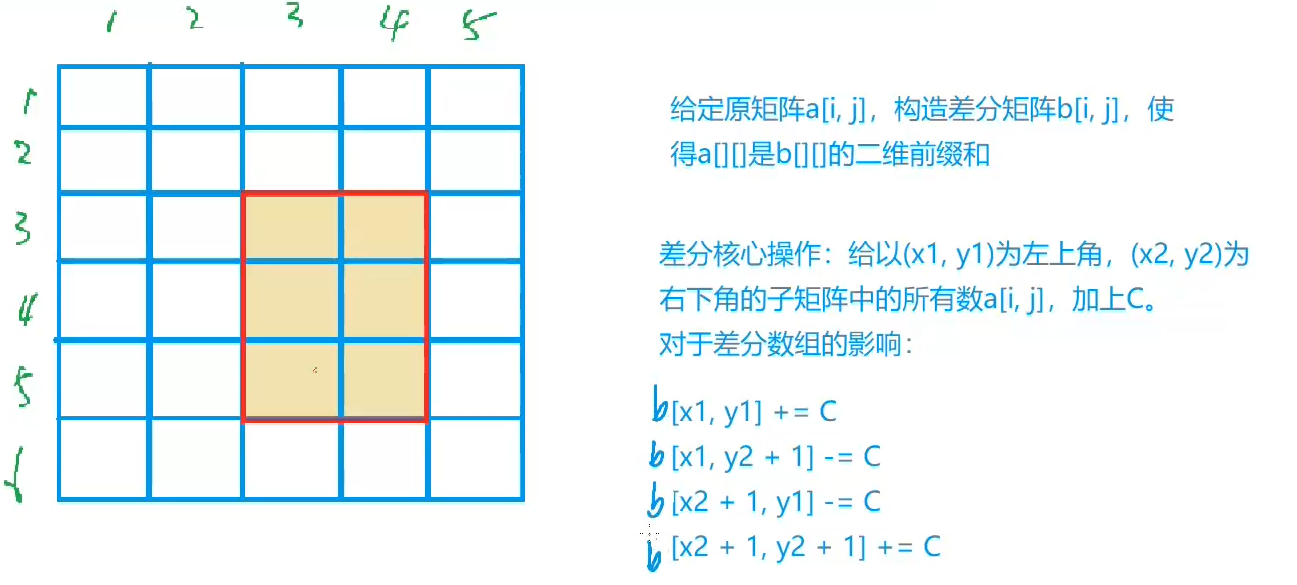
/*对于一个矩阵 a
1 2 4 3
5 1 2 4
6 3 5 9
其二维差分矩阵是
1 1 2 1 4 5 1 3
1 1 1 2

d[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]
差分数组求前缀和就是原数组

解决的问题:
左上角 (x1,y1) 右下角 (x2,y2) 的子矩阵的值都加 c*/

//建立二维差分数组
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){// 建 立 差 分 数 组
cin >>a[i][j];
d[i][j]=a[i][j]-a[i -1][j]-a[i][j -1]+a[i -1][j -1];
}
}

//对二维差分数组进行操作
cin >>x1 >>y1 >>x2 >>y2 >>c;// 左上角 (x1,y1)
// 右下角 (x2,y2) 的矩阵加 c
d[x1][y1 ]+=c;//关系到（x1,y1）的前缀和都要加c,意味着右下方的原数组都加c
d[x1][y2+1] -=c;
d[x2 +1][ y1]-=c;
d[x2 +1][ y2 +1]+=c;

//二维差分数组求前缀和
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
// 差 分 矩 阵 求 前 缀 和 就 是 原 数 组
d[i][j]+=d[i -1][j]+d[i][j-1]-d[i -1][j -1];
cout <<d[i][j]<<" " ;
//a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+b[i][j];
//cout<<a[i][j]<<" ";
}
cout <<endl;
}

#include <iostream> 
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
int n,m,q;
int a[1005][1005];//原数组
int b[1005][1005];//差分数组 
void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}
int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
            //b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];//前缀和的原数组是差分数组 
            insert(i,j,i,j,a[i][j]); 
        } 
    }
    int x1,y1,x2,y2,c;
    while(q--){
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            //差分求前缀和是原数组,差分数组的前缀和数组就是原数组
        b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
        printf("%d ",b[i][j]);
        //a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+b[i][j];
        //printf("%d ",a[i][j]);
        }
        printf("\n");
    }
    return 0;
}