题目描述

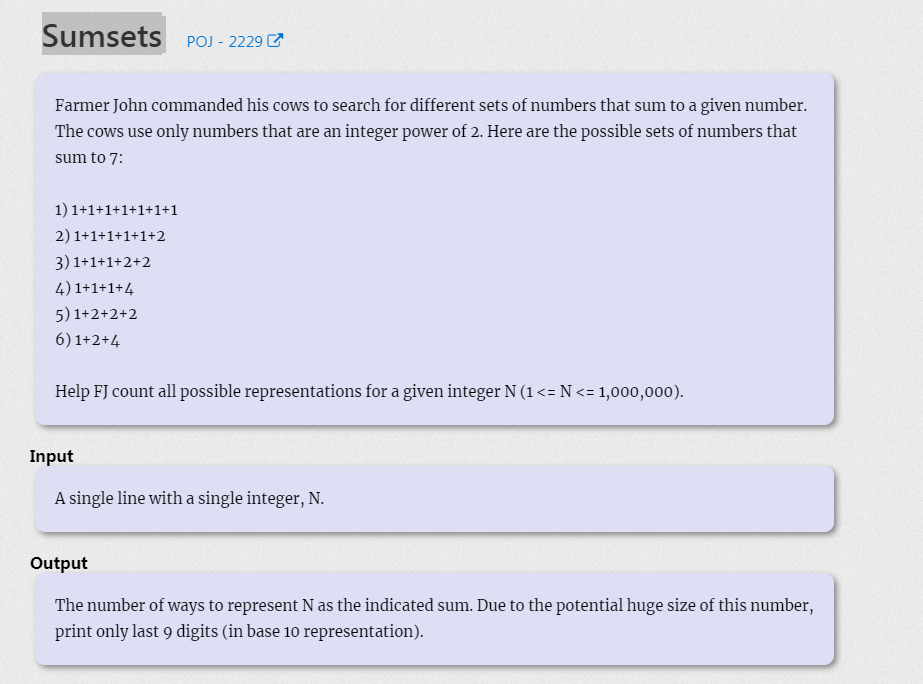
题目大意是输入一个数字 输出以2的幂相加等于它的所有方案,数目较大保留最后九位即可

算法1

解答

根据图中示例 7有6种组合方式

1) 1+1+1+1+1+1+1
2) 1+1+1+1+1+2
3) 1+1+1+2+2
4) 1+1+1+4
5) 1+2+2+2
6) 1+2+4

观察规律

如果输入的数是单数N 那么N的组合方式就是N-1的组合方式再额外添加一个1

如果输入的数字是双数N 那么N的组合方式分为两种 出现1 和不出现1

出现1的组合方式数目就是N-1的组合数目

不出现1的组合方式就是N/2的组合数组(所有组合方式都是N/2的组合元素*2)

C++ 代码

// 112355551111.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include <iostream>


using namespace std;


/*
将一个数N分解为2的幂之和共有几种分法？
Description

Farmer John commanded his cows to search for different sets of numbers that sum to a given number.
The cows use only numbers that are an integer power of 2. Here are the possible sets of numbers that sum to 7:

1) 1+1+1+1+1+1+1
2) 1+1+1+1+1+2
3) 1+1+1+2+2
4) 1+1+1+4
5) 1+2+2+2
6) 1+2+4

Help FJ count all possible representations for a given integer N (1 <= N <= 1,000,000).
*/


const int N = 1000010;
int dp[N];
int n;

int main() {
    cin >> n;
    dp[0] = 1; dp[1] = 1; dp[2] = 2;
    for (int i = 3; i <= n; i++) {
        dp[i] = dp[i - 1];
        if ((i & 1 ) == 0) {
            dp[i] += dp[i / 2];
        }
        dp[i] = dp[i] % 1000000000;
    }
    cout << dp[n] % 1000000000 << endl;

    return 0;
}

我的视频题解空间