题目描述

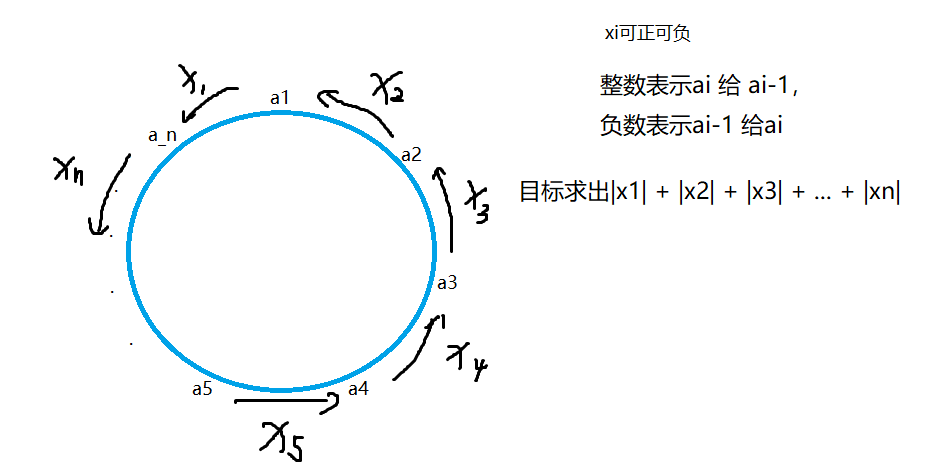
有 n 个小朋友坐成一圈，每人有 a[i] 个糖果。

每人只能给左右两人传递糖果。

每人每次传递一个糖果代价为 1。

求使所有人获得均等糖果的最小代价。

输入格式
第一行输入一个正整数 n，表示小朋友的个数。

接下来 n 行，每行一个整数 a[i]，表示第 i 个小朋友初始得到的糖果的颗数。

输出格式
输出一个整数，表示最小代价。

数据范围
$ 1≤n≤1000000 $,
$ 0≤a[i]≤2×10^9$,
数据保证一定有解。

输入样例：

4
1
2
5
4

输出样例：

4

算法1

(贪心+中位数+数学)

• 我们先对题目进行分析大致画出这样的过程
  

• 将题目进行分析后可以考虑题目的限制条件,本题来说就是对于每个小朋友都获得平均数那么多个糖果，多的给别人，少的等别人给，那么每个小朋友的目标糖果数就是 $\overline{a}$

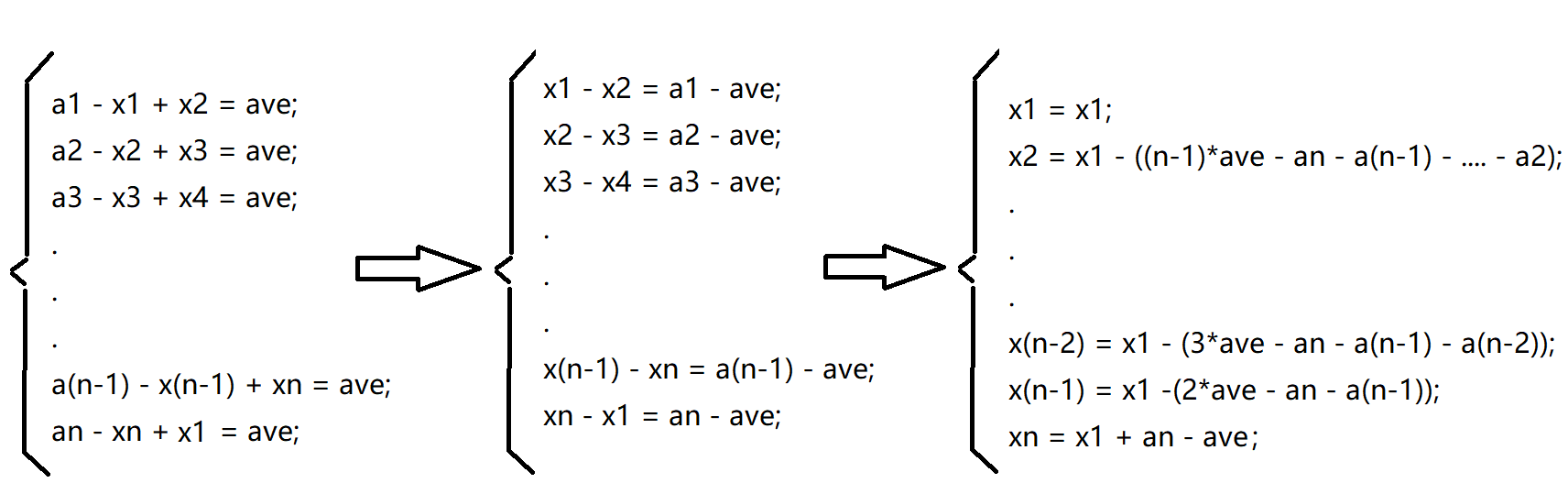
• 将上图最后一步的等式对称到我们的目标式中就可以求出（令$0 = c_1$）
  $ min(|x_1 - c1| + |x_2 - c_2| + |x_3 - c_3| + .... + |x_n - c_n|) $

• 这就转化成了货仓选址问题了

时间复杂度: $O(n)$

C++ 代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;
const int N = 1000010;
typedef long long LL;

int n;
int a[N];
int c[N];

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    LL sum = 0;
    for(int i = 1; i <= n; i ++ ) sum += a[i];

    LL ave = sum / n;

    for(int i = n; i > 1; i -- ) c[i] = c[i + 1] + ave - a[i];
    c[1] = 0;

    sort(c + 1, c + n + 1);

    LL res = 0;
    for(int i = 1; i <= n ;i ++ ) res += abs(c[i] - c[(i + 1) / 2]);

    printf("%lld\n", res);

    return 0;
}