题目描述

经典动态规划问题

给出一个数值均在0~99之间的三角形

请问从第一行的数字出发，每次可选择下一行相邻的两个数字中的一个，
请问达到底层的时候选择的所有数字和最大是多少

输入 第一行一个数字N 表示三角形有N行，后面N行每行有1~N个空格隔开的数字

输出 一行 包含一个答案数字

算法1

动态规划

因为每层每个点都有2中选择(下一行相邻的两个点)

而上一层到达该点的方法也有两种

n层三角形总的路径又有2(n-1) 如果使用dfs求出全部路径再找最大和，时间不允许

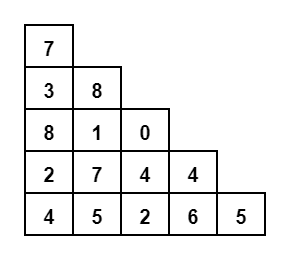
但是我们注意到 上一层两点arr[i-1][j]和arr[i-1][j+1] 到达arr[i][j]的时候 我们肯定选择路径和最大的方案

同样的 arr[i][j]到达下一层两个的选择arr[i+1][j] arr[i+1][j+1]中 我们也肯定选择路径和最大的方案
其余方案忽略

虽然某层的路径和最大比较难以确定，但是第0层选择到第1层的方案是可以快速求得的
然后第1层确定， 再来确定第2层也可以快速求得
如此递推 确定N层求N+1层的最大路径和

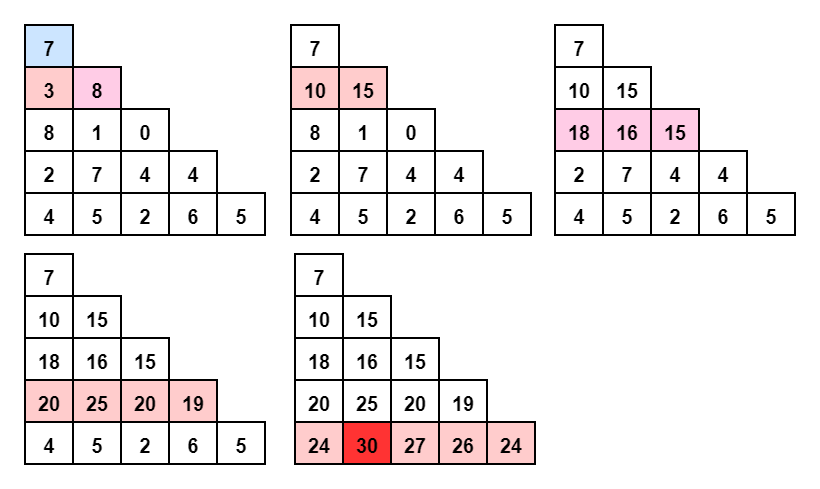
逆向观察 如果三角形只有最下面两层

那么上面一层每个点该如何选择路径使得路径和最大也是可以快速求得

C++ 代码

//由顶向下 和 由底向上 代码
// 1123555.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include <iostream>
#include <algorithm>

using namespace std;


/*
Sample Input
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

Sample Output
30
*/

const int N = 370;
int arr[N][N];
int n;

int main()
{
    cin >> n;

    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= i; j++) {
            cin >> arr[i][j];
        }
    }

#if 1
    for (int i = n - 2; i >= 0; i--) {
        for (int j = 0; j <= i; j++) {
            int val = max(arr[i+1][j], arr[i+1][j + 1]);
            arr[i][j] += val;
        }
    }
    cout << arr[0][0] << endl;
#else
    for (int i = 1; i < n; i++) {
        for (int j = 0; j <= i; j++) {
            int val = arr[i][j];
            if (j < i)
            {
                arr[i][j] = max(arr[i][j], val + arr[i - 1][j]);
            }
            if (j > 0) {
                arr[i][j] = max(arr[i][j], val + arr[i - 1][j - 1]);
            }
        }
    }
    int ans = 0;
    for (int i = 0; i < n; i++) {
        ans = max(ans, arr[n - 1][i]);
    }

    cout << ans << endl;
#endif



    return 0;
}

我的视频空间题解