题目描述

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

样例

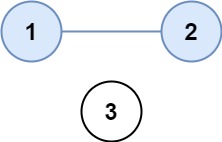
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

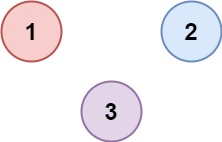
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

限制

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0。
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

算法

(并查集) $O(n^2)$

1. 并查集能解决的一类问题是不断将两个元素所在集合合并，并随时询问两个元素是否在同一集合。
2. 定义数组 $f(i)$ 表示 $i$ 元素所在集合的根结点（代表元素）。初始时，所有元素所在集合的根结点就是自身。
3. 合并时，直接将两个集合的根结点合并，即修改 f 数组。
4. 查询时，不断通过判断 $i$ 是否等于 $f(i)$ 的操作，若不相等则递归判断 $f(f(i))$，直到 $i = f(i)$ 为止。
5. 以上做法会在一条链的情况下单次查询的时间复杂度退化至线性，故可以采用路径压缩优化，将复杂度降到近似常数。读者可以自行查阅相关资料。
6. 对于此题，最后只需检查有多少个元素为一个集合的根结点。

时间复杂度

• 并查集单次操作的复杂度近似于常数，故总时间复杂度为遍历整个朋友关系数组的复杂度，即 $O(n^2)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储并查集。

C++ 代码

class Solution {
private:
    int n;
    vector<int> f;

    int find(int x) {
        return x == f[x] ? x : f[x] = find(f[x]);
    }

    void merge(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx != fy)
            f[fx] = fy;
    }

public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        n = isConnected.size();
        f.resize(n);

        for (int i = 0; i < n; i++)
            f[i] = i;

        for (int i = 0; i < n; i++)
            for (int j = i + 1; j < n; j++)
                if (isConnected[i][j] == 1)
                    merge(i, j);

        int ans = 0;
        for (int i = 0; i < n; i++)
            if (i == find(i))
                ans++;

        return ans;
    }
};