LeetCode 42. 接雨水

题目链接

这两道题是一样的哈
面试题 17.21. 直方图的水量
LeetCode 42. 接雨水

解题思路：双指针

有以下三种情况：递增，两边高中间低，递减

那么其实可以将其划分为两类，因为两边高中间低这种也可以划分成一半递增，一半递减。

解法一：快慢双指针，来回遍历两次

快慢双指针，快指针始终指向比慢指针高的柱子，所以其形成的始终是一个递增的情况，然后根据公式：$$h[i] * (j - i - 1) - (sum[j] - sum[i] - h[j])$$ 计算面积

第一次遍历的面积如下，同理可得，第二次从右边遍历，就会覆盖所有的情况。

C++ 代码

class Solution {
public:
    int sum[100000];
    int trap(vector<int>& h) {
        if(h.size() <= 1)return 0;
        // 获取数组长度
        int n = h.size();
        // 计算前缀和
        sum[0] = h[0];
        for(int i = 1; i < n; i ++)
            sum[i] = sum[i-1] + h[i];
        int i = 0, j = 0;
        int res = 0;
        while(j < n-1)
        {
            j++;
            if(h[j] >= h[i])
            {
                res += h[i] * (j - i - 1) - (sum[j] - sum[i] - h[j]);
                i = j;
            }
        }
        if(i != j){
            i = n-1,j = n-1;
            while( j > 0 )
            {
                j--;
                if(h[j] > h[i])
                {
                    res += h[i] * (i - j - 1) - (sum[i] - sum[j] - h[i]);
                    i = j;
                }
            }
        }
        return res;
    }
};

解法二：左右指针，一次遍历

要想盛水，要求左右边界的柱子大于中间的柱子。

乘多少水，取决于左右最高的柱子的最小值。

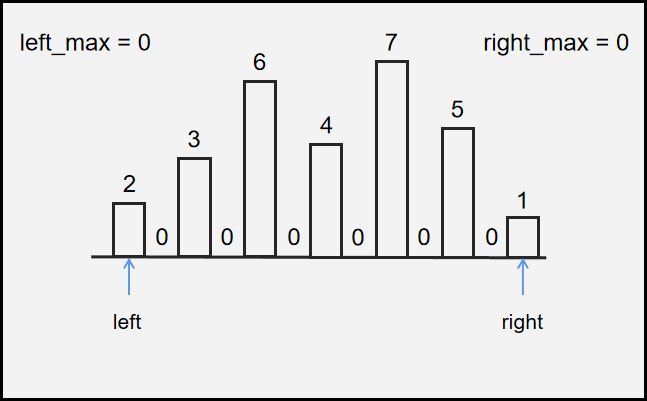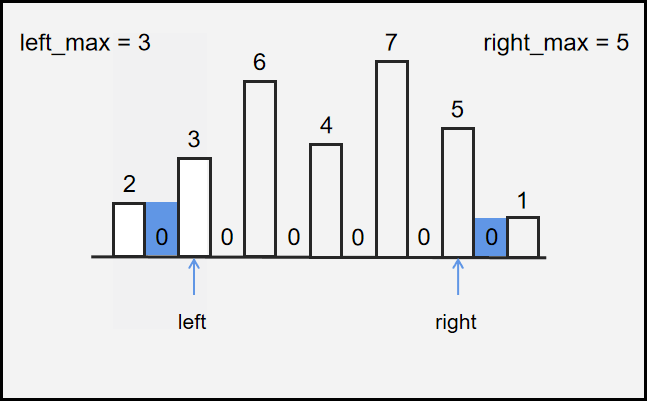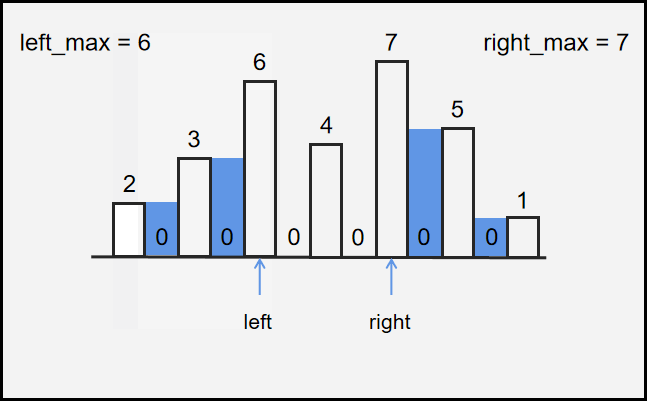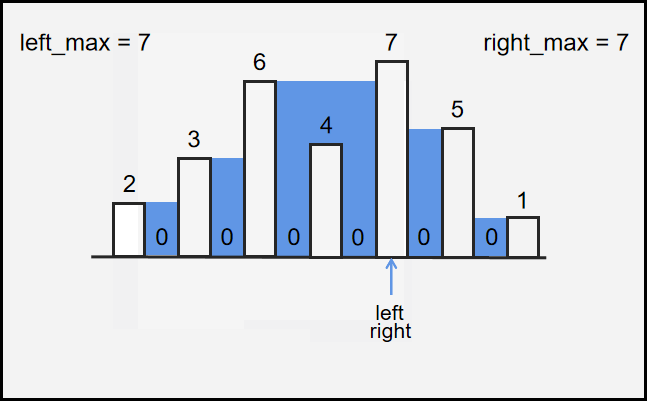
所以使用左右双指针$left$，$right$ ，分别从左右两边开始往中间遍历，并且使用$left_max$ ，$right_max$ 来记录左右指针分别遍历过的所有值的最大值。

每次迭代：

1. 判断$h[left]$ 与 $h[right]$ 的大小关系。
2. 小的判断当前 $h$ 值是否大于其方向的最大值
   大于：说明其方向本身最大left_max = h[left];
   小于：说明左右都有比他的可以盛水ans = (left_max - h[left])
3. 小的往前走一步，直到$left$，$right$ 相遇

证明正确性：

• $left，right$ 指向左右边界，假如$h[left] < h[right]$ 说明$h[right]$ 大于$left$ 左边的任意一个数，
• 由于$left_max$ 记录了$left$ 遍历过的最大值
  $left+1$ 之后是有可能大于$left_max$ 的，
  假如没有大于，则说明$left+1$ 之后的柱子是可以盛水的，盛水的面积就是$(left_max - h[left]) * 1$
  假如$h[left + 1] > h[right]$ 则说明当前$h[left]$ 大于右边$right$ 遍历过的任意一个数
• 同理保证了，停止的指针，大于正在走的指针遍历过的任何一个数，所以保证了$(left_max - h[left]) * 1$ 的正确性

C++ 代码

class Solution {
public:
    int trap(vector<int>& h) {
        int n = h.size();
        int left_max = 0,right_max = 0;
        int left = 0 , right = n-1;
        int ans = 0;
        while(left < right)
        {
            if(h[left] < h[right])
            {
                if(h[left] < left_max){
                    ans += (left_max - h[left]);
                }else{
                    left_max = h[left];
                }
                left++;
            }else{
                if(h[right] < right_max){
                    ans += (right_max - h[right]);
                }else{
                    right_max = h[right];
                }
                right--;
            }
        }
        return ans;
    }
};