原题链接：完全二叉树的权值

题目描述

给定一棵包含 $N$ 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 $A_1,A_2,⋅⋅⋅A_N$，如下图所示：

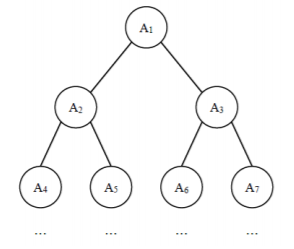
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？

如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 $1$。

输入格式

第一行包含一个整数 $N$。

第二行包含 $N$ 个整数 $A_1,A_2,⋅⋅⋅A_N。$

输出格式

输出一个整数代表答案。

数据范围

$1≤N≤105,$
$−105≤Ai≤105$

输入样例1：

7
1 6 5 4 3 2 1

输出样例1：

2

思路

因为是完全二叉树，那么每一层的起始点是 $2^{(n - 1)}$ ，每一层的终止点为 $2^n - 1$ 。其中 $n$ 为层数

所以可以利用双指针，每一次对某一层的权值相加即可

因为是求区间和，也可以利用前缀和，求出起始点到终止点的和即可

双指针

时间复杂度

$O(n)$

C++ 代码

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 100010;
int tr[N];
int n;

int main()
{
    cin >> n;
    for(int i = 1;i <= n;i ++) scanf("%d",&tr[i]);

    int res = 1;
    int maxv = -N;
    int depth = 1;
    for(int i = 1;i <= n;i *= 2) {
        LL cnt = 0;
        for(int j = i;j <= i * 2 - 1 && j <= n;j ++) cnt += tr[j];
        if(cnt > maxv) {
            maxv = cnt;
            res = depth;
        }
        depth ++;
    }

    cout << res << endl;
    return 0;
}

前缀和

时间复杂度

$O(n)$

C++ 代码

#include <iostream>
using namespace std;

typedef long long LL;

const int N = 100010;
LL s[N];
int n;

int main()
{
    cin >> n;
    for(int i = 1;i <= n;i ++) {
        int x;
        scanf("%d",&x);
        s[i] = s[i - 1] + x;
    }

    int maxv = - N;
    int depth = 1;
    int res = 1;
    LL sum = 0;
    for(int i = 1;i <= n;i *= 2) {
        int j = i * 2 - 1;
        if(j <= n) sum = s[i * 2 - 1] - s[i - 1];
        else sum = s[n] - s[i - 1];
        if(sum > maxv) {
            maxv = sum;
            res = depth;
        }
        depth ++;
    }

    cout << res << endl;
    return 0;
}