• 此时仍然需要使用时间戳以及$dfn、low$数组。

• 首先我们需要考虑如何求割点？考虑DFS过程中从点u遍历到点j，如果有$dfn[u] \le low[j]$，则：

① 如果x不是根节点，那么x是割点；

② 如果x是根节点，则至少存在两各个节点y，使得$low[y_i] \ge dfn[x]$，此时x才是割点。

• 如何求点连通分量（v-DCC）呢？

首先如果一个点是一个孤立点的话，也是一个v-DCC；

做法类似于有向图求SCC，可以使用一个栈记录当前边连通分量中的点，如果在DFS过程中从点u遍历到点j，有$dfn[u] \le low[j]$，说明u可能是割点，具体步骤如下：

if (dfn[u] <= low[j]) {
    cnt++;  // cnt记录u的子树的个数
    if (x非根 || cnt > 1) x是割点;
    将栈中元素弹出直至弹出y为止;
    u也属于该v-DCC;
}

• 我们可能对下图存在疑问，下图中j是割点，u不是v-DCC中的点？

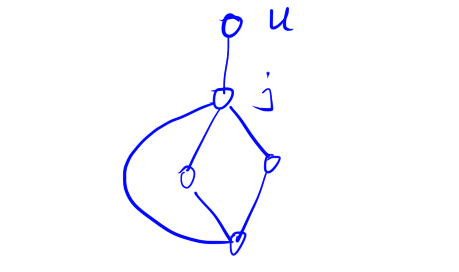
• 上图中其实u也是v-DCC中的点，但是上图有两个v-DCC，如下图：

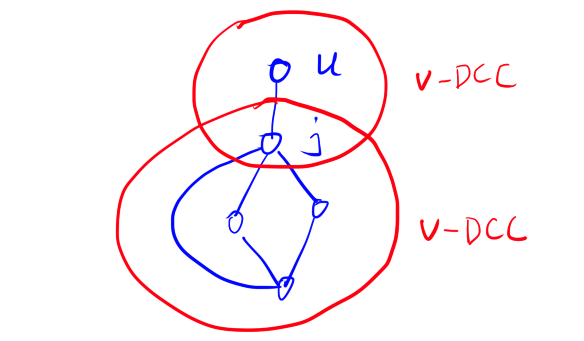
分析

• 本题相当于问：给定一个无向图，问最少在几个点上设置出口，可以使得不管其他哪个点被删除，其余所有点都可以与某个出口连通。

• 本题中给的无向图可能不是连通的，存在多个连通分量，我们不需要考虑连通分量的情况，我们考虑每个v-DCC即可。如果某个连通分量中不含有割点，则该连通分量就是一个v-DCC，对应下面的情况（1）。

• 假设每个v-DCC的需要设置的通道数记为$res[i]$，方案数为$num[i]$，则最终整个图需要的通道数为$res = \sum res[i]$，方案数为$num = \prod num[i]$。首先，我们的出口数量必须有$res \ge 2$，否则只存在一个出口的话，万一出口坏了，则其他点都出不去了。下面我们聚焦讨论每个v-DCC（假设当前讨论的第i个v-DCC点的数量为size个，割点数量为cnt个，这可以使用tarjan算法求解）。

（1）如果v-DCC中不含有割点（这种情况对应图中某个连通分量中不存在割点），即cnt==0，则需要设置两个出口（$res[i]=2$），这两个出口可以任意选两个，方案数$num[i]=C_{size}^2$。

（2）如果v-DCC中有割点，即cnt>1，则需要对该v-DCC所在的连通分量进行缩点操作（实际代码中不需要进行缩点，只需要计算cnt即可，这里为了分析方便），这里的缩点规则是：每个割点单独作为一个点；从每个v-DCC向其所包含的每个割点连边。如下图（缩点后至少存在三个点，我们不需要考虑单独的割点，考虑割点所在的v-DCC即可）：

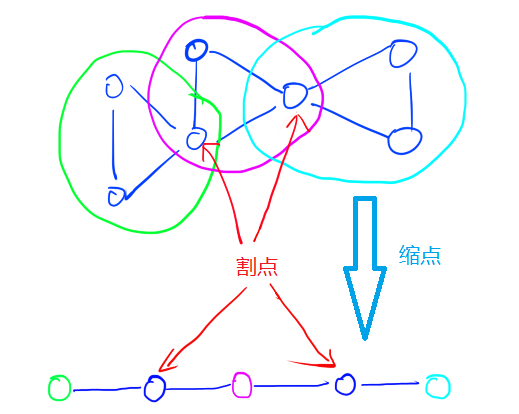
缩点之后边的个数不会增加，但是点的数量可能增加，新图中点的个数=连通分量的个数+割点的数目，因此最多有2倍的点。

如上图，因为这个连通分量存在割点，因此存在v-DCC，具体来说，上图对应的连通分量3个v-DCC，我们需要依次考虑每个v-DCC。

（2.1）如果cnt==1，如上图中的绿色和青色对应的缩点，这个割点相当于出口，则我们需要在该v-DCC中出除了割点的位置外设置一个出口即可，方案数为size-1；这样能保证该v-DCC的安全，因为如果割点坏了，通过该v-DCC中的出口该v-DCC中的其他点可以出去；如果这个出口坏了，可以通过这个割点到达其他v-DCC，也可以通过其他v-DCC设置的出口安全出去。

（2.2）如果cnt>=2，如上图中的紫色对应的缩点，则该v-DCC不需要设置任何出口；因为无论该v-DCC中的哪个点坏了，都可以通过割点到达其他v-DCC，然后通过其他v-DCC设置的出口安全出去。

• 最后我们还需要考虑孤立点的情况，孤立点不是割点，我们在孤立点也需要设置一个出口，否则若其他点坏了，这各孤立点没法通过出口出去。

• 另外这一题没有给点数，但是是从1开始的自然数，我们需要自己求一下点数。

#include <iostream>
#include <cstring>
#include <vector>

using namespace std;

typedef unsigned long long ULL;

const int N = 1010, M = 1010;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
int dcc_cnt;  // v-DCC的个数
vector<int> dcc[N];  // 存储每个v-DCC有哪些点，之后用来求每个v-DCC中割点的数量
bool cut[N];  // 记录每个点是不是割点
int root;  // 记录每个连通块的"根节点"

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {

    dfn[u] = low[u] = ++timestamp;
    stk[++top] = u;

    // 判断点u是否为孤立点
    if (u == root && h[u] == -1) {
        dcc[++dcc_cnt].push_back(u);
        return;
    }

    int cnt = 0;  // u的不能回到u之前的子树数量
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
            if (dfn[u] <= low[j]) {
                cnt++;
                /* 判断割点对应两种情况：
                         /
                        u
                       / \
                      o   o
                */
                if (u != root || cnt > 1) cut[u] = true;

                ++dcc_cnt;
                int y;
                do {
                    y = stk[top--];
                    dcc[dcc_cnt].push_back(y);
                } while (y != j);
                dcc[dcc_cnt].push_back(u);
            }
        } else 
            low[u] = min(low[u], dfn[j]);
    }
}

int main() {

    int T = 1;
    while (cin >> m, m) {

        // 因为存在多组测试数据，需要初始化变量
        for (int i = 1; i <= dcc_cnt; i++) dcc[i].clear();
        idx = n = timestamp = top = dcc_cnt = 0;
        memset(h, -1, sizeof h);
        memset(dfn, 0, sizeof dfn);
        memset(cut, 0, sizeof cut);

        while (m--) {
            int a, b;
            cin >> a >> b;
            n = max(n, a), n = max(n, b);
            add(a, b), add(b, a);
        }

        // 求v-DCC
        for (root = 1; root <= n; root++)
            if (!dfn[root])
                tarjan(root);

        int res = 0;  // 最少需要设置的出口数量
        ULL num = 1;  // 方案数
        for (int i = 1; i <= dcc_cnt; i++) {
            int cnt = 0;  // 该v-DCC对应的割点数目
            int t = dcc[i].size();  // 当前v-DCC中点的数量
            for (int j = 0; j < t; j++)
                if (cut[dcc[i][j]])
                    cnt++;

            if (cnt == 0) {
                if (t == 1) res++;
                else res += 2, num *= t * (t - 1) / 2;
            } else if (cnt == 1)
                res++, num *= t - 1;
        }

        printf("Case %d: %d %llu\n", T++, res, num);
    }

    return 0;
}