分析

• 我们将可以放置骨牌的格子看成点，可以放置骨牌的两个格子之间连一条边。则问题就转化为了：最多取多少条边，所有选出的边无公共点。相当于让我们求最大匹配。我们还要判断这个图是不是二分图。

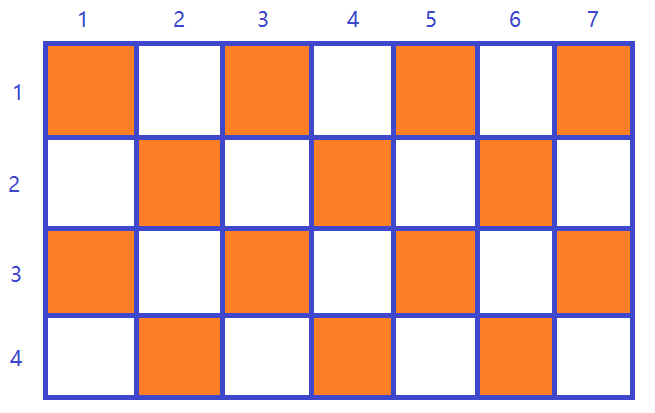
• 因为：一个图是二分图$\iff$这个图可以二染色。我们需要判断棋盘是否可以二染色即可，对于棋盘，存在一种经典的二染色方式，如下图：

• 由上面分析可知，任意的棋盘都满足二染色，对应的图是二分图，所以此时就可以使用匈牙利算法求解了。

• 那么如何判断每个格子的颜色呢？我们可以给每个格子一个编号，等于横纵坐标之和，和为偶数的是一种颜色，和为奇数的是另一种颜色。我们枚举偶点或者奇点都可以。

#include <iostream>
#include <cstring>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;

const int N = 110;

int n, m;  // 边长、不能放置的点的数量
bool g[N][N];  // 为true代表有障碍物
PII match[N][N];  // 存储第二个集合中的每个点 当前 匹配的第一个集合中的点是哪个
bool st[N][N];  // 表示第二个集合中的每个点是否已经被遍历过

int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

bool find(int x, int y) {

    for (int i = 0; i < 4; i++) {
        int a = x + dx[i], b = y + dy[i];

        if (a < 1 || a > n || b < 1 || b > n) continue;
        if (st[a][b] || g[a][b]) continue;
        st[a][b] = true;

        PII t = match[a][b];
        if (t.x == 0 || find(t.x, t.y)) {
            match[a][b] = {x, y};
            return true;
        }
    }
    return false;
}

int main() {

    cin >> n >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        g[a][b] = true;
    }


    int res = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) 
            if ((i + j) % 2 && !g[i][j]) {
            memset(st, 0, sizeof st);
            if (find(i, j)) res++;
        }

    cout << res << endl;

    return 0;
}