算法题目

题目链接
给定一个长度为n的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式

第一行包含整数n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

1≤n≤100000

输入样例：

6
2 3 4 5 6 1

输出样例：

5

算法思路

求逆序对的算法是利用了归并排序的思想,在归并排序的过程中会将序列分为两部分，此时逆序对可以分为三种情况：两个数都在左边的（设为s1）。两个数都在右边的（s2），一个数在左边一个数在右边的(s3)。现在假设我们在归并排序的时候写的函数merge_sort(int[] arr, int l, int r)可以返回l到r区间中逆序对数量。那么s1=mergeSort(a, l, mid),s2=mergeSort(a, mid + 1, r);，s3很显然没有直观的答案。

那么核心问题就在于怎么求s3，以及怎么使我们的merge_sort(int[] arr, int l, int r)可以返回l到r区间中逆序对数量。

算法实现

怎么求s3?

s3可以看作下图中红色圈圈的情况。对于右边的中的任意一个数，在左边的数只要大于他就构成逆序对，我们只能要统计出这些数，就能求出s3。

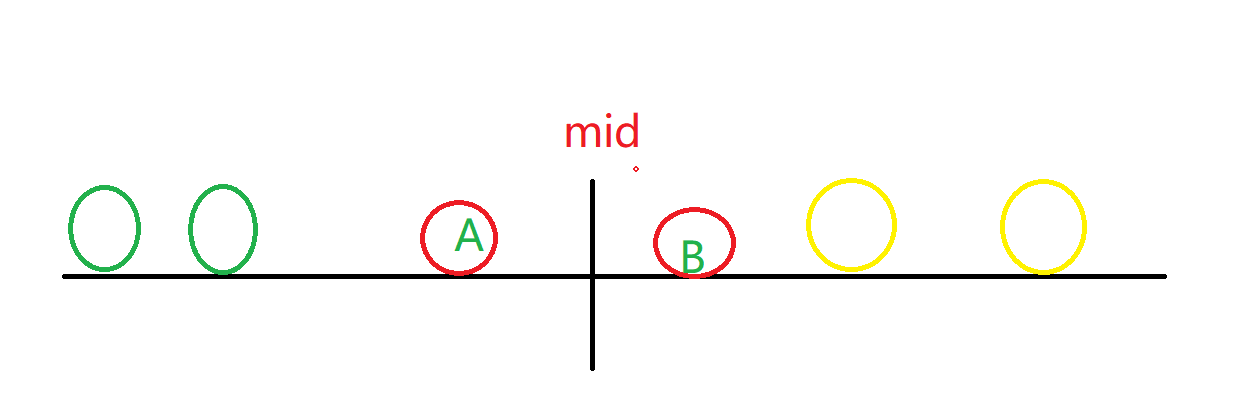
如何能快速地统计出来这些数呢？我们知道在归并排序中，左右两边都是排序好的数列。因此，对于右图中的B我们只需要找到左边第一个大于B的数A，那么A后面的数都是大于B的。假设A的下标为i，不难得到我们要统计的数目为：mid-i+1,恰巧在归并排序的合并过程中正好有两边序列依次比大小的过程:

if (arr[i] <= arr[j])
    tmp[k++] = arr[i++];
else
    tmp[k++] = arr[j++];

else中的语句即代表左边数列中的数大于右边中的数了，我们可以在此时将mid-i+1加到总答案中去。那么s3的问题就解决了。

if (a[i] <= a[j])
    tem[k++] = a[i++];
else {
    res += mid - i + 1;
    tem[k++] = a[j++];
}

s3的问题解决后，我们的函数还没有解决问题的能力，只需要在递归出口的时候return 0;因为递归结束的时候数列中只有一个数了，不存在逆数对。还需要在递归归并排序的时候统计两边的逆序对数量之和long res = mergeSort(a, l, mid) + mergeSort(a, mid + 1, r);即可。

这里注意一点，因为题目中的数据范围最大是100000,一般对于数据范围大于10w的题目就要考虑数据溢出、时间复杂度等问题。

那么对于最大100000规模的数据，逆序对最多的数量为多少呢？

当数列是一个倒序的数列时应该是逆序对数量最大的时候，每一个数可以和他后面所有的数形成逆数对，如果有n个数，那么总的逆序对数量为：(n-1)+(n-2)+……+1即$\frac{n(n-1)}{2}$个，大约$\frac{n^2}{2}$个，代入10w的数据范围得最多逆数对个数为：$5\times10^9$，这个数据大于int的范围。所以这个题用int的话会溢出，我们采用long来存结果。

java代码实现

import java.io.InputStreamReader;
import java.util.Scanner;

public class Main {

    public static void main(String[] args)  {
        Scanner sacnner = new Scanner(new InputStreamReader(System.in));
        int n = sacnner.nextInt();
        int[] a = new int[n];
        for (int i = 0; i < n; i++) {
            a[i] = sacnner.nextInt();
        }
        System.out.println(mergeSort(a, 0, n - 1));
        sacnner.close();
    }

    private static long mergeSort(int[] a, int l, int r) {
        if (l >= r)
            return 0;

        int mid = l + r >> 1;
        long res = mergeSort(a, l, mid) + mergeSort(a, mid + 1, r);
        int tmp[] = new int[r-l+1];
        int k = 0, i = l, j = mid + 1;
        while (i <= mid && j <= r) {
            if (a[i] <= a[j])
                tmp[k++] = a[i++];
            else {
                res += mid - i + 1;
                tmp[k++] = a[j++];
            }
        }
        while (i <= mid)
            tmp[k++] = a[i++];
        while (j <= r)
            tmp[k++] = a[j++];
        for(i=l,j=0;i<=r;i++,j++)a[i]=tmp[j];
        return res;
    }

}