Multiple Sequences

题意

1. 给定两个正整数n和m
2. 问能够构造出多少个长为n的序列A, 而且1 <= A[i] << m, A[i + 1] % A[i] == 0.
3. 最后答案模998244353
4. 范围n, m范围是 [0, 2e5]

题解

1. 不同的数字的个数不会超过$\log _{2} m$个
2. 假设sum[i]表示在范围[1,m]中选出i个数 且 满足 A[i + 1] % A[i] == 0的选个数 (先选择)
3. 枚举我们的序列A中有几种不同的数, 设为k, 即把n个数分为k部分, 即$C_{n-1}^{k-1}$种 (选择完成后排列)
4. 答案是
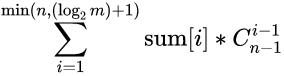
5. 设f[i][j]表示在[1,i]中选择j个数, 满足A[i + 1] % A[i] == 0, 且i必选的方案数.
6. i的倍数与i之间的转移方式: f[i * t][j + 1] += f[i][j];
7. sum[i]的答案是

Show me the code

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
typedef long long LL;
const int MOD = 998244353;
const int N = 2e5 + 100;
int f[N][20], sum[N];
int fact[N], infact[N];
int n, m;

// 通过预处理逆元的方式求组合数:
int qmi(int a, int k, int p)
{
    int res = 1;
    while(k)
    {
        if(k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

void Combination(){
    fact[0] =  infact[0] = 1;
    for(int i = 1; i < n; i ++)
    {
        fact[i] = (LL)fact[i - 1] * i % MOD;
        infact[i] = (LL)infact[i - 1] * qmi(i, MOD - 2, MOD) % MOD;
    }
}

int calcu(int a, int b){
    return (LL)fact[a] * infact[b] % MOD * infact[a - b] % MOD;
}

int main(){
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= m; i ++) f[i][1] = 1;
    for(int i = 1; i <= m; i ++){
        for(int j = 1; j < 20; j ++){
            for(int k = i + i; k <= m; k += i){
                f[k][j + 1] = (f[k][j + 1] + f[i][j]) % MOD;
            }
        }
    }
    // 预处理组合数
    Combination();
    // log 以2为底, log_{2} 200000 大约是 17.6, 取19必定不会超过
    int t = min(19, n);
    // 计算sum[i]
    for(int i = 1; i <= t; i ++){
        for(int j = 1; j <= m; j ++){
            sum[i] = (sum[i] + f[j][i]) % MOD;
        }
    }
    // 统计最后数据
    int ans = 0;
    for(int i = 1; i <= t; i ++){
        //cout << i << " " << sum[i] << " " << calcu(n - 1, i - 1) << endl;
        ans = (ans + 1ll * sum[i] * calcu(n - 1, i - 1)) % MOD;
    }
    printf("%d\n", ans);
    return 0;
}

Reference