并查集大致讲解

开始时每个集合都是一个独立的集合,并且都是等于自己本身下标的数
例如:
p[5]=5,p[3]=3;
如果是M操作的话那么就将集合进行合并,合并的操作是:
p[3]=p[5]=5;
所以3的祖宗节点便成为了5
此时以5为祖宗节点的集合为{5，3}
如果要将p[9]=9插入到p[3]当中,应该找到3的祖宗节点,
然后再把p[9]=9插入其中,所以p[9]=find(3);(find()函数用于查找祖宗节点)
也可以是p[find(9)]=find(3),因为9的节点本身就是9
此时以5为祖宗节点的集合为{5,3,9};
如果碰到多个数的集合插入另一个集合当中其原理是相同的
例如:
上述中以5为祖宗节点的是p[5],p[3],p[9];(即p[5]=5,p[3]=5,p[9]=5)
再构造一个以6为祖宗节点的集合为{6,4，7，10}
如果要将以6为祖宗节点的集合插入到以5为祖宗节点的集合,则该操作可以是
p[6]=find(3)（或者find(9),find(5)）
此时p[6]=5
当然如果是以6为祖宗节点集合中的4,7,10则可以这样
p[find(4)]=find(3)
或者p[find(7)]=find(3)均可以
此时以6为祖宗节点的集合的祖宗节点都成为了5

#include<bits/stdc++.h>
using namespace std;
const int N=100100;
int p[N];
int find(int a)
{
    if(p[a]!=a)p[a]=find(p[a]);//注意眼睛睁大看清楚啊，这里是find(p[a])不是find(a)啊，这样就递归去找
//a的祖宗节点了，直到p[某]==a为止，然后沿途过程当中每一个p[a]，p[某]都指向了祖宗节点，这样使后续的查找
//过程当中时间复杂度为O(1)
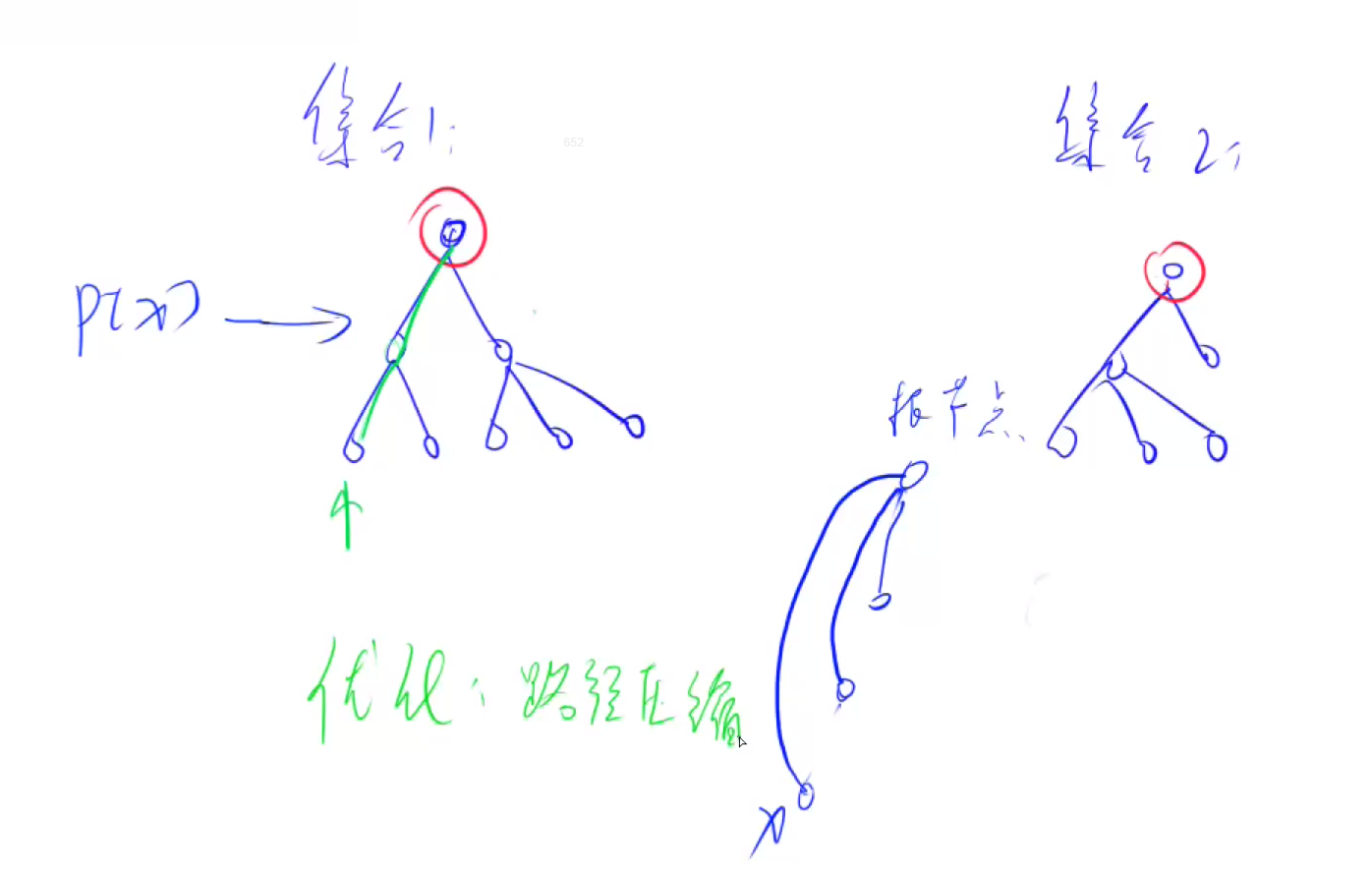
//这是一个寻找祖先节点+状态压缩的一行关键代码
    return p[a];
}
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)p[i]=i;
    while(m--)
    {
        char x;
        int a,b;
        cin>>x>>a>>b;
        if(x=='M')
        {
            p[find(a)]=find(b);//写成p[find(b)]还是find(b)都一样，find返回的是祖宗节点的编号
//p[find(b)]就是祖宗节点的编号的值，祖宗节点的编号的值就是祖宗节点的编号，所以这里写哪个都行
        }
        else
        {
            if(find(a)==find(b))cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }
    }
    return 0;
}