剑指 Offer 53 - II. 0～n-1中缺失的数字

博文地址

题目链接：

LeetCode 剑指 Offer 53 - II. 0～n-1中缺失的数字

Acwing 68. 0到n-1中缺失的数字

思路：

一般二分的查找条件：

1. 顺序存储
2. 元素有序

该题满足了一般二分查找的条件

因为需要存储的的数有n个数，但是数组只有n-1个位置，所有必然有一个数会丢失

该题满足二分的性质：可以将这个区间分成一个有丢失数的区间，一个没有丢失数的区间。

二分最难的在于怎么检查他的性质。

任取一个数x，如果在数组中<= x 的个数等于x+1，那么说明丢失的数是大于x的

而这个题目很特殊，只要检查当前索引是否等于存储的值即可判断。可得：

if(nums[mid] == mid) 可得缺失的值大于mid

虽然二分的是索引，但是索引的值跟存储的值是相等的，结果也是当前索引的值。但是有一个种特殊情况，就是当缺失的是最后一个数的时候，其整个区间的都是没有缺失的，所以是找不到缺失的那个数的，其指针最终停留在最后一个位置上，但其并不是最终的答案。

如： [0] 缺失1

​ [1,2,3] 缺失4

所以我们可以在最终结果判断其idx是否等于val ，如果相等则缺失的是最后一个数

易理解

class Solution {
public:

    int missingNumber(vector<int>& nums) {
        int l = 0, r = nums.size()-1;

        while( l < r )
        {
            int mid = l + r >> 1;
            if(nums[mid] == mid) l = mid + 1;
            else r = mid;
        }
        if(r == nums[r])return l + 1;
        else return l;
    }
};

也可以根据以下代码进行改进：

① 将判断条件改为while(l <= r) 其在最后l = r的时候还会进行一次操作，这样如果最后一个数是相等的，其会再最后的结果上+1

② 但是这样会进入死循环：所以也要更改一下else r = mid - 1

可能会疑惑，这样会不会丢失正确的值。其实不会。

证明：

只有当题目的运算结果为r = mid的时候进行r = mid -1 才会丢失正确的值。

接下来证明r = mid - 1 不会丢失答案：

第一种情况：正常的情况 例子：[0,1,3]

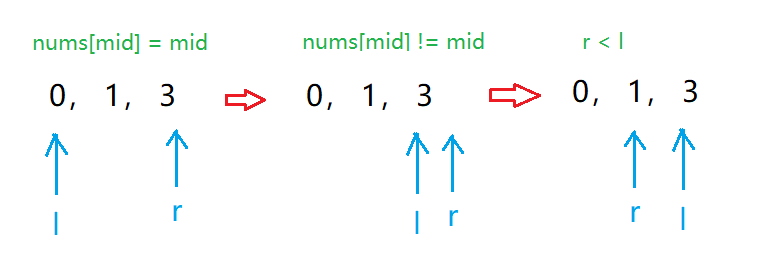
第二种情况：r = mid 例子：[0,1,3,4,5]

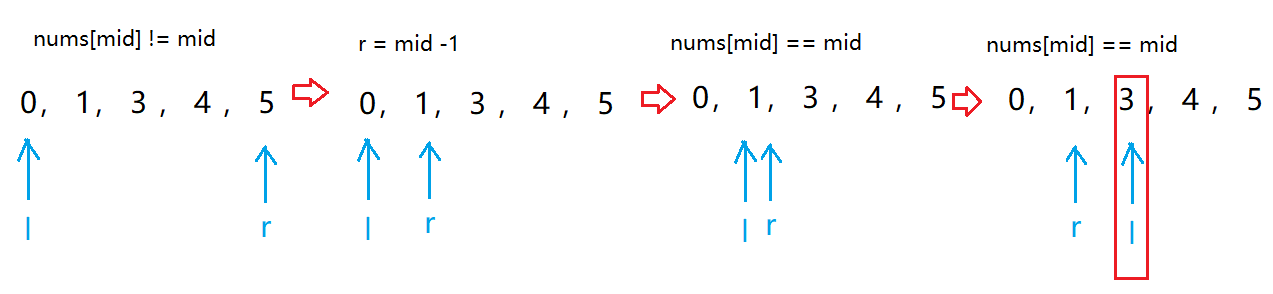
如果结果为r = mid 进行 r = mid -1 的操作丢失了，之后l、r 最后会停留在r-1的位置，而因为上面①l == r 的时候会再进行一次操作，而且是满足if(nums[mid] == mid ) 这个条件的，所以l会再加1，则l为最后的结果

改进代码：

class Solution {
public:

    int missingNumber(vector<int>& nums) {
        int l = 0, r = nums.size()-1;

        while( l <= r )
        {
            int mid = l + r >> 1;
            if(nums[mid] == mid) l = mid + 1;
            else r = mid - 1;
        }
        return l;
    }
};