算法1

(最小割)

第一问：
根据最大流最小割定理第一问直接求最大流即可
第二问：
类似于双关键字排序，将容量作为第一关键字，边数作为第二关键字，将边原容量设为10000倍+1，第一关键在高位，第二关键字在低位且边数只有1000，不会影响第一关键字，直接求最小割，最小割后四位即为最小边数
第三问：
要求字典序最小，从小到大遍历所有边，判断该边是否可为最小割的割边

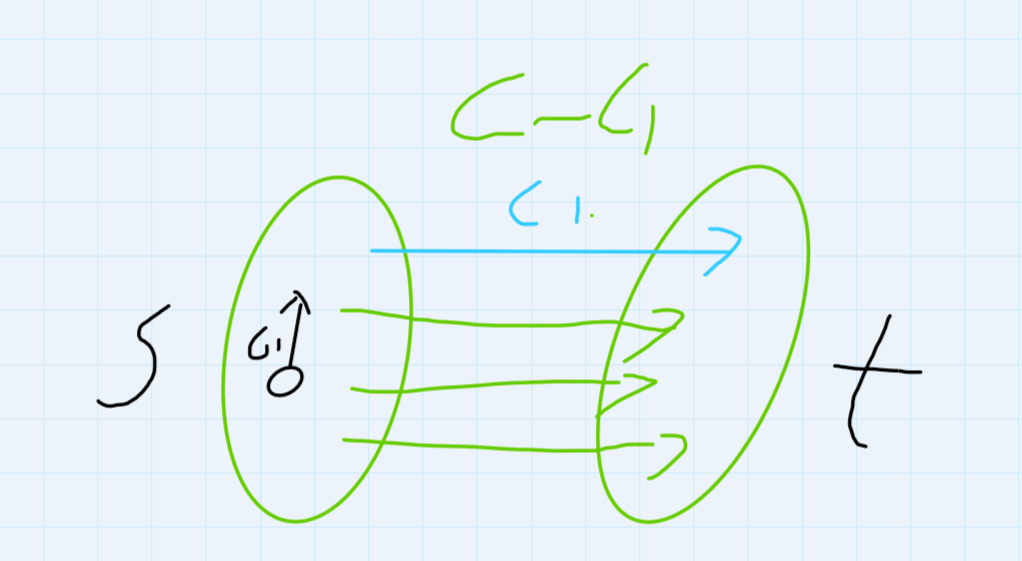
若删除的边容量为C1，求删除该边之后的最小割，若最小割为 C - C1则表示该边为割边，若该边不为割边（图中黑边）则原网络中最小割为C - C1矛盾；
将确定的割边删去，继续往后判断，将可以为割边的边输出即可

C++ 代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
#include<cmath>
#include<string>
#include<cstring>
#include<bitset> 
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<iomanip>
#include<algorithm>
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define endl "\n"
#define int long long
#define PI  acos(-1)
//CLOCKS_PER_SEC clock()函数每秒执行次数
using namespace std;

const int INF = 0x3f3f3f3f;
const int N = 3e5+5,M = N * 2;
int mod = 1e9 +7;
int n,m,k,S,T;
int e[M],ne[M],f[M],h[N],idx;
void add(int a,int b,int c){
    e[idx] = b,f[idx] = c,ne[idx] = h[a],h[a] = idx++;
    e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx++;
}
int d[N],cur[N];
bool bfs(){
    queue<int> q;
    q.push(S);
    memset(d,0,sizeof(d));
    d[S] = 1,cur[S] = h[S];
    while(!q.empty()){
        int u = q.front();q.pop();
        for(int i = h[u] ; ~i ; i = ne[i]){
            int ver = e[i];
            if(!d[ver] && f[i]){
                d[ver] = d[u] + 1;
                cur[ver] = h[ver];
                if(ver == T) return true;
                q.push(ver); 
            }
        }
    }
    return false;
}
int find(int u,int limit){
    if(u == T) return limit;
    int flow = 0;
    for(int i = cur[u] ; ~i && flow < limit ; i = ne[i]){
        int ver = e[i];
        cur[u] = i;
        if(d[ver] == d[u] + 1 && f[i]){
            int k = find(ver,min(f[i],limit - flow));
            if(!k) d[ver] = 0;
            f[i] -= k,f[i ^ 1] += k,flow += k;
        }
    }
    return flow;
} 
int dinic(){
    int r = 0,flow;
    while(bfs()) while(flow = find(S,INF)) r += flow;
    return r;
}
void init(){
    for(int i = 0 ; i < idx ; i += 2){
        f[i] += f[i ^ 1];
        f[i ^ 1] = 0;
    }
}
void solve(){
    cin >> n >> m;
    S = 1,T = n;
    memset(h,-1,sizeof(h));
    while(m--){
        int a,b,c;
        cin >> a >> b >> c;
        //双关键字排序每个的容量设为10000c + 1
        //c在高位为第一关键字，1为边数在低位为第二关键字
        //最大有1000条边所以第二关键字不影响第一关键字
        add(a,b,c * 10000 + 1);
    }
    int res = dinic();
    cout << res / 10000 << ' ' << res % 10000 << endl;
    for(int i = 0 ; i < idx ; i += 2){
        //还原残留网络
        init();
        //删除第i条边判断最小割的减少值是否为该边容量
        //若成立则表示该边可为割边，将该边删去，继续找割边
        int t = f[i];
        f[i] = 0;
        int d = dinic();
        if(d == res - t){
            cout << i / 2 + 1 << endl;
            res = d;
        }
        //该边不可为割边复原
        else f[i] = t;
    }
}

signed main(){
    IOS;
    solve();
    return 0;
}
/*
*
*　　┏┓　　　┏┓+ +
*　┏┛┻━━━┛┻┓ + +
*　┃　　　　　　　┃
*　┃　　　━　　　┃ ++ + + +
*  ████━████+
*  ◥██◤　◥██◤ +
*　┃　　　┻　　　┃
*　┃　　　　　　　┃ + +
*　┗━┓　　　┏━┛
*　　　┃　　　┃ + + + +Code is far away from 　
*　　　┃　　　┃ + bug with the animal protecting
*　　　┃　 　 ┗━━━┓ 神兽保佑,代码无bug　
*　　　┃ 　　　　　　 ┣┓
*　　  ┃ 　　　　　 　┏┛
*　    ┗┓┓┏━┳┓┏┛ + + + +
*　　　　┃┫┫　┃┫┫
*　　　　┗┻┛　┗┻┛+ + + +
*/