卡特兰数

• 卡特兰数：首先这个一个数，很多问题的结果都是卡塔兰数，比如2016年全国三卷数学选择题压轴题让求解的就是卡特兰数，问题如下（AcWing 889. 满足条件的01序列也是这个题）：

• 首先是结论：卡特兰数为:

$$ \frac{C_{2n} ^ n}{n+1} $$

• 因此，对于上面的题目，结果就是

$$ \frac{C_{2m} ^ m}{m+1} = \frac{C_8 ^ 4}{4+1} = \frac{70}{5} = 14 $$

因此选择C。

• 下面看一下卡特兰数的公式是如何推导出来的。首先我们需要将上述问题转换成一个等价的问题：在一个二维平面内，从(0, 0)出发到达(n, n)，每次可以向上或者向右走一格，0代表向右走一个，1代表向上走一格，则每条路径都会代表一个01序列，则满足任意前缀中0的个数不少于1个数序列对应的路径则右下侧，如下图：

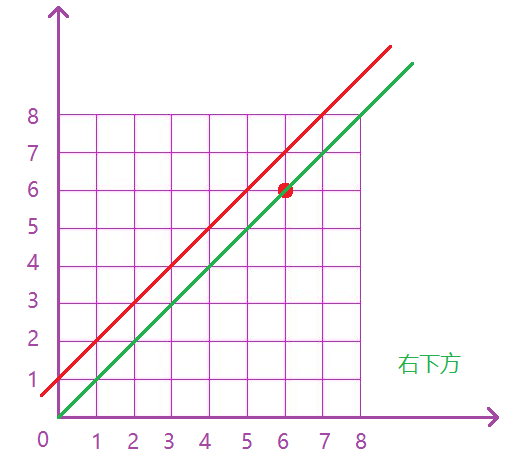
符合要求的路径必须严格在上图中红色线的下面（不可以碰到图中的红线，可以碰到绿线）。则我们考虑任意一条不合法路径，例如下图：

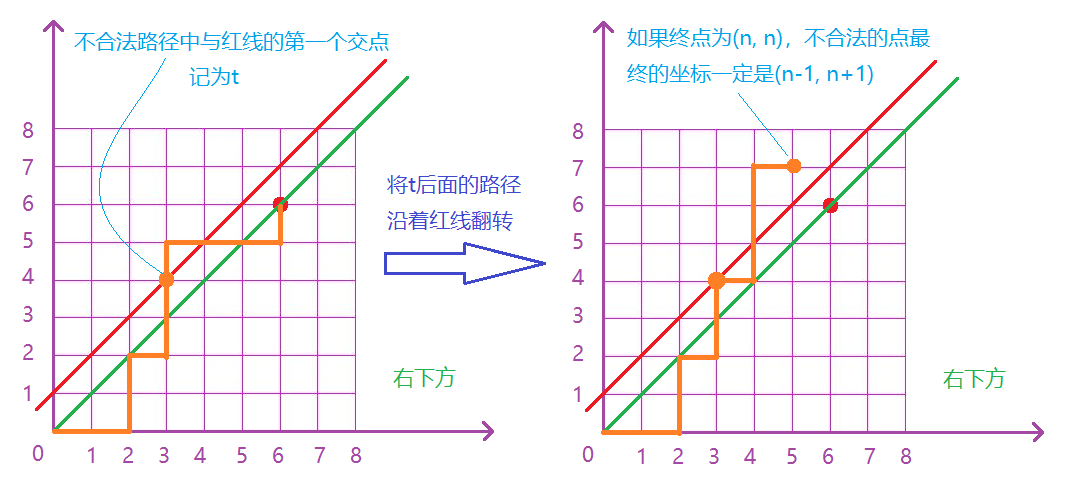
所有路径的条数为 $C_{2n}^{n}$，其中不合法的路径有 $C_{2n}^{n-1}$ 条，因此合法路径有：
$$ C_{2n}^{n} - C_{2n}^{n-1} = \frac{(2n)!}{n! \times n!} - \frac{(2n)!}{(n+1)! \times (n-1)!} \\\\ = \frac{(2n)! \times (n+1)}{n! \times (n+1)!} - \frac{(2n)! \times n}{n! \times(n+1)!} \\\\ = \frac{(2n)! \times (n+1) - (2n)! \times n}{n! \times (n+1)!} \\\\ = \frac{(2n)!}{n! \times (n+1)!} = \frac{1}{n+1} \times \frac{(2n)!}{n! \times n!} \\\\ = \frac{C_{2n} ^ n}{n+1} $$
推导完毕。

• 除了上述两种问题，如下问题对应的答案也是卡特兰数：

（1）n个结点的二叉树数量h(n) ；其实有递推公式，即：
$$ h(n) = \sum _{i=1}^{n} h(i-1) \times h(n-i) \quad \quad h(0)=1 $$
（2）矩阵链乘：$P=A_1 \times A_2 \times … \times A_n$，有多少种不同的计算次序？（相当于加括号，问合法括号序列有多少个）

（3）一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?

（4）有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)

• 补充内容：

分析

• 本题让求卡特兰数，直接带入公式即可：

$$ \frac{C_{2n} ^ n}{n+1} = \frac{1}{n+1} \times \frac{a \times (a-1) \times … \times (a-b+1)}{1 \times 2 \times … \times b} \quad \quad a=2n, \ b=n $$

• 因为mod是质数，因此任何数与mod都互质，可以使用快速幂求逆元，否则需要使用扩展欧几里得算法求逆元。

代码

#include <iostream>

using namespace std;

typedef long long LL;

const int mod = 1e9 + 7;

int qmi(int a, int k, int p) {

    int res = 1 % p;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int main() {

    int n;
    cin >> n;

    int a = 2 * n, b = n;
    int res = 1;

    for (int i = a; i > a - b; i--) res = (LL)res * i % mod;
    for (int i = 1; i <= b; i++) res = (LL)res * qmi(i, mod - 2, mod) % mod;

    res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;

    cout << res << endl;

    return 0;
}