Blog
题目
思路


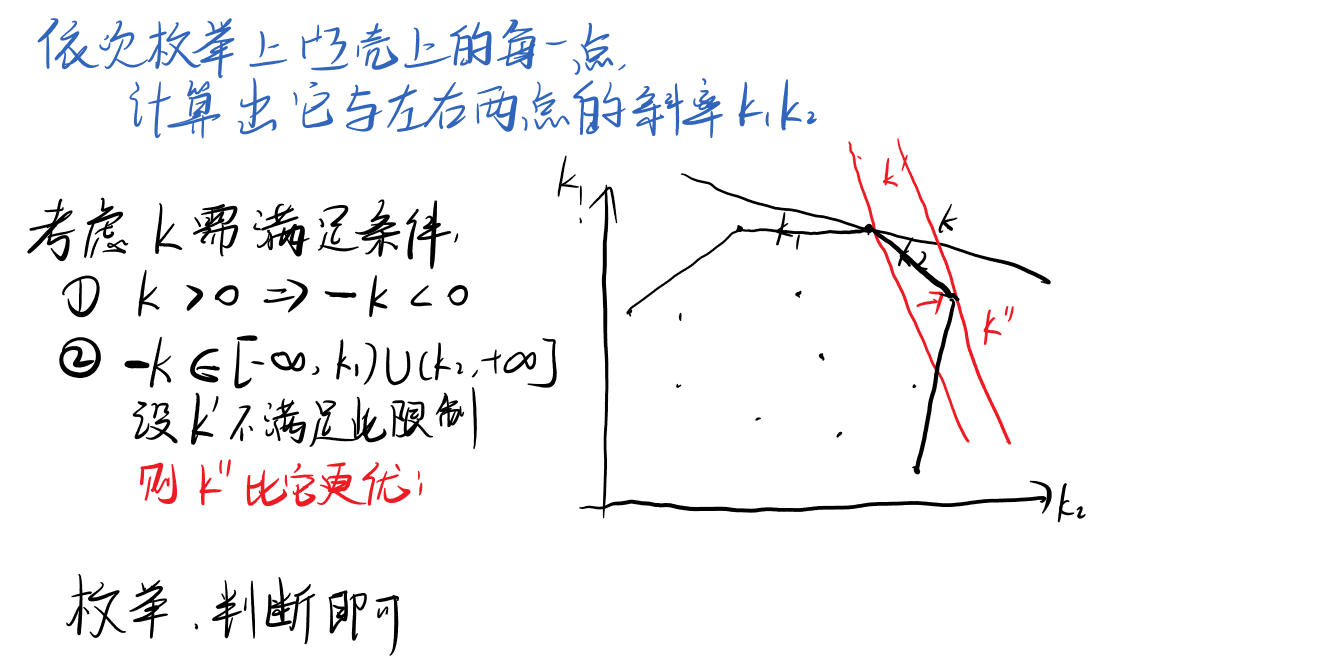
代码
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const int N = 2000010;
const double eps = 1e-8;
int n, stk[N], top;
struct PDD { double x, y; } P[N];
bool PDD_cmp(PDD a, PDD b) { return (a.x != b.x) ? a.x < b.x : a.y < b.y; }
PDD operator+(PDD a, PDD b) { return (PDD) { a.x + b.x, a.y + b.y }; }
PDD operator-(PDD a, PDD b) { return (PDD) { a.x - b.x, a.y - b.y }; }
double cro(PDD a, PDD b) { return a.x * b.y - a.y * b.x; }
double dot(PDD a, PDD b) { return a.x * b.x + a.y * b.y; }
double area(PDD a, PDD b, PDD c) { return cro(b - a, c - a) / 2; }
// 求斜率, 注意特判斜率不存在的情况, 返回INF即可
double get_k(PDD a, PDD b) { return (a.x == b.x) ? 1e18 : (a.y - b.y) / (a.x - b.x); }
// 求函数 f, 注意特判, 如果 k <= 0, 不合法不要算, 防止更新错误答案
double f(PDD a, double k) { return k > 0 ? (a.x + a.y + a.x * k + a.y / k) : 1e18; }
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%lf%lf", &P[i].x, &P[i].y);
sort(P + 1, P + n + 1, PDD_cmp);
for (int i = 1; i <= n; stk[++top] = i, i++) // 求个凸包
while (top >= 2 && area(P[stk[top - 1]], P[stk[top]], P[i]) >= 0) top--;
double res = 1e18;
for (int i = 1; i <= top; i++) {
PDD A = P[stk[i]], B = P[stk[i - 1]], C = P[stk[i + 1]];
double k = sqrt(A.y / A.x), k1 = get_k(B, A), k2 = get_k(C, A);
// 以下不要忘记带负号
if ((i == 1 || -k <= k1) && // 要么 i = 1, 没有前驱节点, 要么比 k1 小
(i == top || -k >= k2)) // 要么 i = top, 没有后继节点, 要么比 k2 大
res = min(res, f(A, k)); // 这样满足 k 的条件, 更新答案
else if (i > 1) res = min(res, f(A, -k1));
else if (i < top) res = min(res, f(A, -k2));
}
printf("%.4lf", res);
return 0;
}

