题目描述

在一个 m x n 的网格上有一个球，给定球的起点坐标 (i, j)，你每次可以将这个球移动到四个方向（上下左右）相邻的格子上或者移出网格边界。然而，你最多可以移动 N 次。求出所有可以将球移出网格边界的路径数量。答案数可能很大，返回模 $10^9+7$ 后的结果。

样例

输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6

解释:

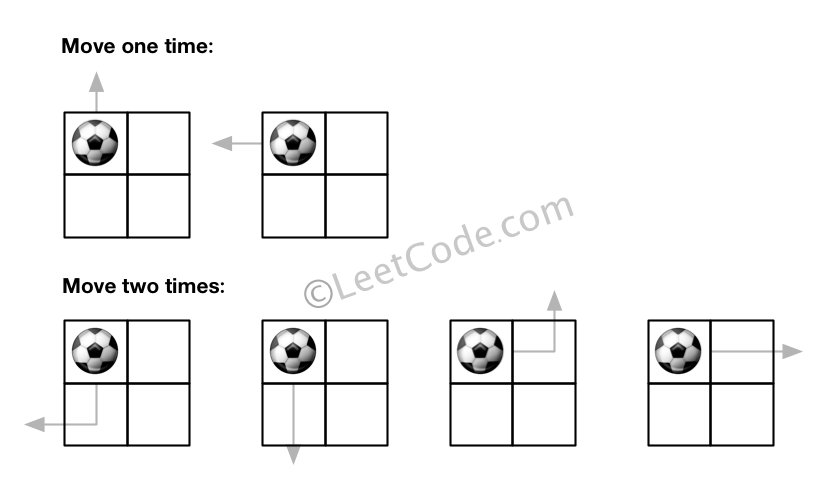
输入: m = 1, n = 3, N = 3, i = 0, j = 1
输出: 12

解释:

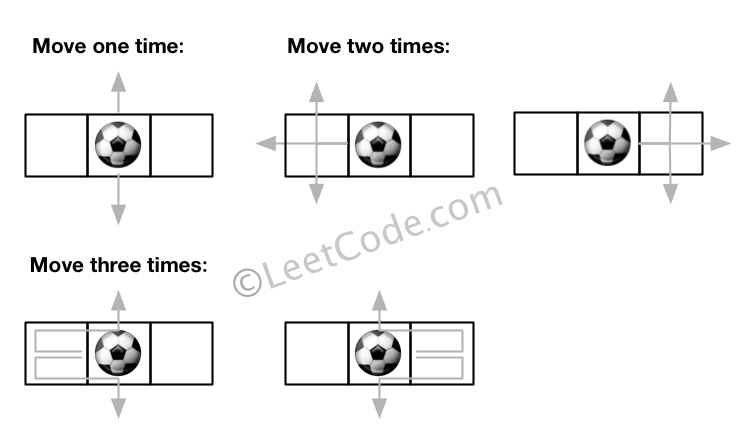
注意

• 一旦将球移出网格边界，不可再移动回来。
• 网格长和宽在 [1, 50] 的范围内。
• N 在 [0, 50] 的范围内。

算法

(动态规划) $O(N \cdot m \cdot n)$

1. 定义状态 $f(k, x, y)$ 表示从网格边界格子经过 $k$ 步，到达格子 (x, y) 的方案数。
2. 初始时，每个位于边界的格子 (x, y)，其 $f(0, x, y) = 1$；转移时，每个点可以从四个相邻的格子（如果存在）进行累加转移。
3. 最终答案为，$f(0, i, j) + f(1, i, j) + … + f(N-1, i, j)$。由于规定边界的格子步数为 0，所以最多只能统计到 $N-1$ 步。

时间复杂度

• 状态数为 $O(N \cdot m \cdot n)$，每个状态的转移数为 $O(1)$，故总时间复杂度为 $O(N \cdot m \cdot n)$。

C++ 代码

class Solution {
public:
    int mod = 1000000007;
    int dx[4] = {0, 1, 0, -1};
    int dy[4] = {1, 0, -1, 0};

    int findPaths(int m, int n, int N, int i, int j) {
        if (N == 0)
            return 0;
        vector<vector<vector<int>>> f(N, vector<vector<int>>(m, vector<int>(n, 0)));

        for (int x = 0; x < m; x++) {
            f[0][x][0] ++;
            f[0][x][n - 1]++;
        }

        for (int y = 0; y < n; y++) {
            f[0][0][y]++;
            f[0][m - 1][y]++;
        }

        for (int k = 1; k < N; k++)
            for (int x = 0; x < m; x++)
                for (int y = 0; y < n; y++)
                    for (int t = 0; t < 4; t++) {
                        int u = x + dx[t], v = y + dy[t];
                        if (u < 0 || u >= m || v < 0 || v >= n)
                            continue;
                        f[k][x][y] = (f[k][x][y] + f[k - 1][u][v]) % mod;
                    }
        int ans = 0;
        for (int k = 0; k < N; k++)
            ans = (ans + f[k][i][j]) % mod;
        return ans;
    }
};