算法

(数学、组合) $O(n\log n)$

先对数组 $A$ 进行升序排序，原数组就变为 $\{A_1’, A_2’, \dots, A_n’\}$，我们需要的答案就是

$$\prod_{i = 1}^n (A_i’ - A_{i - 1}’ + 1)$$

其中 $A_0’ = 0$。

当 $N = 1$ 时，有 $A_1 + 1$ 种

当 $N = 2$ 时，有 $(\min(A_1, A_2)) * (\max(A_1, A_2) - \min(A_1 - A_2) + 1)$ 种

例如，$A1 = 3$，$A2 = 5$，两栋楼都有1楼，2楼和3楼，第二栋楼有四楼，答案为12种

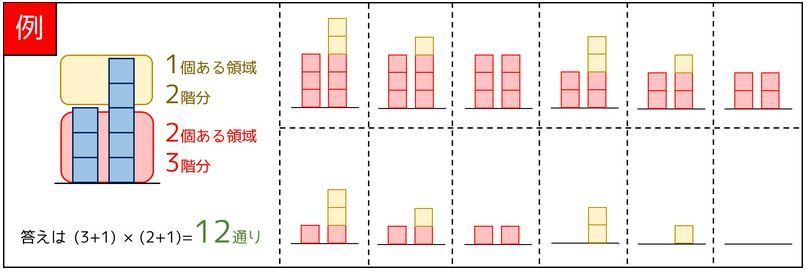
当 $N = 3$ 时：
先对原数组排序，变成 $A1’, A2’, A3’$，我们需要的答案就是 $(A_1’ + 1)(A_2’ - A_1’ + 1)(A_3’ - A_2’ + 1)$
例如，$A = (3, 2, 4)$ 的情况，可得到答案为12种。

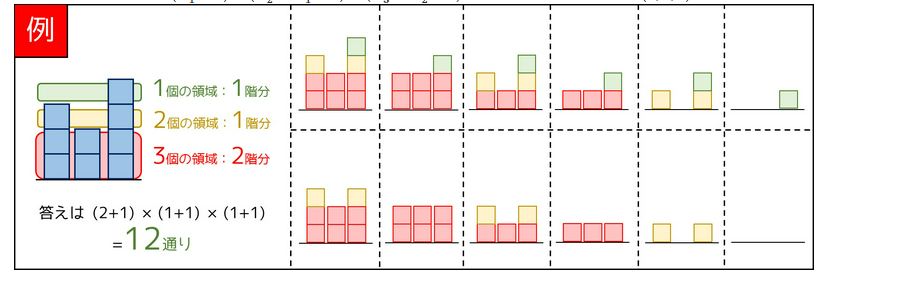
然后可以通过归纳法得出问题的答案。

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define rng(a) a.begin(), a.end()

using std::cin;
using std::cout;
using std::vector;
using std::istream;
using std::ostream;
using ll = long long;

// const int mod = 998244353;
const int mod = 1000000007;
struct mint {
    ll x;
    mint(ll x=0):x((x%mod+mod)%mod) {}
    mint operator-() const {
        return mint(-x);
    }
    mint& operator+=(const mint a) {
        if ((x += a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator-=(const mint a) {
        if ((x += mod-a.x) >= mod) x -= mod;
        return *this;
    }
    mint& operator*=(const mint a) {
        (x *= a.x) %= mod;
        return *this;
    }
    mint operator+(const mint a) const {
        return mint(*this) += a;
    }
    mint operator-(const mint a) const {
        return mint(*this) -= a;
    }
    mint operator*(const mint a) const {
        return mint(*this) *= a;
    }
    mint pow(ll t) const {
        if (!t) return 1;
        mint a = pow(t>>1);
        a *= a;
        if (t&1) a *= *this;
        return a;
    }

    // for prime mod
    mint inv() const {
        return pow(mod-2);
    }
    mint& operator/=(const mint a) {
        return *this *= a.inv();
    }
    mint operator/(const mint a) const {
        return mint(*this) /= a;
    }
};
istream& operator>>(istream& is, mint& a) {
    return is >> a.x;
}
ostream& operator<<(ostream& os, const mint& a) {
    return os << a.x;
}

int main() {
    int n;
    cin >> n;

    vector<int> a(n);
    for (auto& it : a) cin >> it;
    sort(rng(a));

    mint ans = 1;
    int pre = 0;
    rep(i, n) {
        int x = a[i] - pre;
        pre = a[i];
        ans *= x + 1;
    }

    cout << ans << '\n';

    return 0;
}`