详情请看注释！

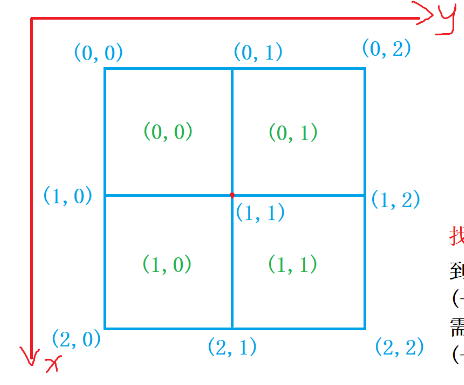
坐标对应关系如图：

• 图片来源：@小呆呆 题解
  

参考代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <deque>

using namespace std;

const int N = 510;

typedef pair<int, int> PII;

char g[N][N];
int T, n, m, dist[N][N], vis[N][N];
// 四个对角线的点的方向
int dx[] = {-1, -1, 1, 1}, dy[] = {-1, 1, 1, -1};
// 四个对象线方向
int ix[] = {-1, -1, 0, 0}, iy[] = {-1, 0, 0, -1};

/*
    每个点不仅会入队出队一次！---> 与堆优化dijkstra算法一样！
        ---> 本质：边权不仅仅有一种，若只有一种边权，则只会入队出队一次，即入队的时候就是最小值！
            可以画一个三角形理解！

        ①--0-- ②        1号点 更新 2，3号点，3号点还不是最小
         \    / 0   
        1 \  /
           ③

        ①--1-- ②        1号点 更新 2，3号点，3号点一定最小
         \    / 1   
        1 \  /
           ③

    双端队列主要解决图中边的权值 只有两种权值 的最短路问题 -> 可以保证单调性和两段性！
        写法类似堆优化dijkstra算法！

    队列的单调性和两段性！
        处于理想状态 0 -> 入队头
        处于非理想状态 1 -> 入队尾  ---> 即需要旋转电线才能继续走！

    起点为(0, 0)，由于每走一步，必然是横纵坐标都加一，因此能走到的点一定是横纵坐标相加为偶数的点！
        若终点横纵坐标相加为奇数，则一定不可达！
*/

int bfs(){
    deque<PII> dq;
    dq.push_back({0, 0});
    memset(dist, 0x3f, sizeof dist);
    memset(vis, false, sizeof vis);
    dist[0][0] = 0;

    // 中心点可走的四个方向 \\ 代表一个 \ .
    char c[5] = "\\/\\/";

    while(dq.size()){
        auto t = dq.front();
        dq.pop_front();

        // 与一般bfs不一样，出队才能确定每个点的最小值
        if(t.first == n && t.second == m) return dist[n][m];

        // 类似dijkstra,处理过就不用在处理了
        if(vis[t.first][t.second]) continue;
        vis[t.first][t.second] = true;

        for(int i = 0; i < 4; i ++){
            int tx = t.first + dx[i], ty = t.second + dy[i];
            // 边数为 n，因此点数为 n + 1
            if(tx >= 0 && tx <= n && ty >= 0 && ty <= m){
                // 该点四个方向在g数组坐标
                int gx = t.first + ix[i], gy = t.second + iy[i];
                // 只有当前不是处于理想状态才需要 权值 + 1
                int w = (g[gx][gy] != c[i]);
                int d = dist[t.first][t.second] + w;

                if(d < dist[tx][ty]){
                    dist[tx][ty] = d;
                    if(!w) dq.push_front({tx, ty}); // 处于理想状态 0
                    else dq.push_back({tx, ty});    // 处于非理想状态 1
                }
            }
        }
    }
    return -1;
}

int main(){
    cin >> T;
    while(T --){
        cin >> n >> m;
        for(int i = 0; i < n; i ++) cin >> g[i];
        // 奇数终点一定无法到达！
        if(n + m & 1) cout << "NO SOLUTION" << endl;
        else cout << bfs() << endl;
    }
    return 0;
}