分析

• 用求卡特兰数的方法分析一下这个题目就可以得到答案，关于卡特兰数的分析：网址。

• 我们需要求出点(n, m)关于y = x + 1对称的点的坐标，假设为(a, b)，则任何一种不合法的方案都可以转化为到达(a, b)的路径，如下图：

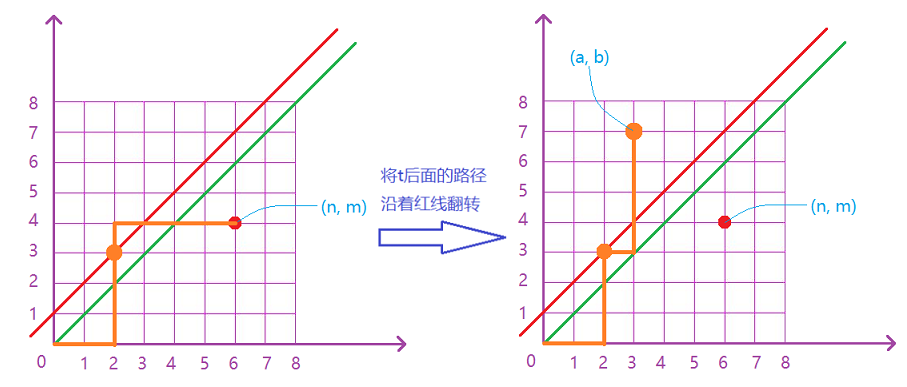
• 则答案为：$C_{m+n}^{n} - C_{m+n}^{a}$，问题就转变为了如何求解坐标(a, b)。这是高中知识，我们可以列方程求解，根据垂直可以得到一个等式，根据线段中点在对称轴上可以得到另一个等式，可以得到：

$$ \begin{cases} 1 \times \frac{b - m}{a - n} = -1 \\\\ \frac{b + m}{2} = \frac{a + n}{2} + 1 \end{cases} $$

解方程可得：a = m - 1, b = n + 1。

• 因此答案为：

$$ C_{m+n}^{n} - C_{m+n}^{m - 1} $$

• 本题需要使用到高精度求解，如果递推的话计算量为$10000^2=1 \times 10^8$，再加上高精度计算会超时，因此这里求解阶乘的方式然后带入公式求组合数，类似于AcWing 888. 求组合数 IV。

代码

#include <iostream>

using namespace std;

const int N = 100010;

int primes[N], cnt;
bool st[N];
int a[N], b[N];  // C(m+n, n)结果存储在a中, C(m+n, m-1)结果存储在b中

// 筛质数
void init(int n) {

    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

// 返回n中质因数p的个数
int get(int n, int p) {

    int s = 0;
    while (n) s += n / p, n /= p;
    return s;
}

// 高精度乘法
void mul(int r[], int &len, int x) {

    int t = 0;
    for (int i = 0; i < len; i++) {
        t += r[i] * x;
        r[i] = t % 10;
        t /= 10;
    }
    while (t) {
        r[len++] = t % 10;
        t /= 10;
    }
}

// 返回组合数C(x, y)，结果存储在r中, r[0]是最低位
int C(int x, int y, int r[]) {

    int len = 1;
    r[0] = 1;

    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        int s = get(x, p) - get(y, p) - get(x - y, p);
        while (s--) mul(r, len, p);
    }

    return len;
}

// 高精度减法
void sub(int a[], int al, int b[], int bl) {

    for (int i = 0, t = 0; i < al; i++) {
        a[i] -= t + b[i];
        if (a[i] < 0) a[i] += 10, t = 1;
        else t = 0;
    }
}

int main() {

    init(N - 1);

    int n, m;
    cin >> n >> m;

    // 求出C(m+n, n)结果存储在a中, C(m+n, m-1)结果存储在b中
    int al = C(n + m, m, a);  // al是数据a的长度
    int bl = C(n + m, m - 1, b);  // bl是数据b的长度

    // C(m+n, n) - C(m+n, m-1)，结果存储在a中
    sub(a, al, b, bl);

    int k = al - 1;
    while (!a[k]) k--;
    while (k >= 0) printf("%d", a[k--]);

    return 0;
}