简述树状数组【举例为区间求和】

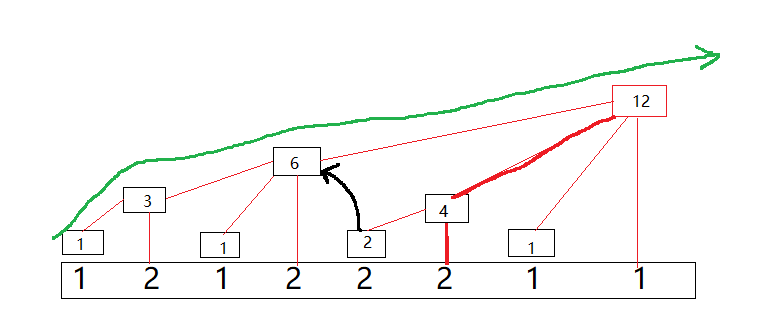
1. update(i,x),a[i]改变x(增加或减少)或者写作add(i,x)更明确，更新路径如上图红色粗线所示，从当前位置向最大下标方向，逐个做+x更新
2. query(i) 返回1到i区间上的某个性质，如黑色粗线。例如查询i=5,向一的方向走累加当前值，找到绿色线时，会直接返回[绿色线像山的脊背，他本身就是区间1到i的值]，因此最长查找步数就是当前下标找到绿色线的步数

3. 值得注意的是每次增大或减小的步长和当前下标有关，即lowbit(i)，

   • i的二进制写法，从低位到高位连续零的个数为k，则lowbit(i) =2^k，
   • 比如i=10=(1010)->k=1->lowbit(i)=2^1=2可以验证10&（-10）=1010&0110=（10）=2

思路

模拟很容易写，主要当得到上次出现的下标lasti和当前下标i，每次要遍历区间[lasti+1,i-1],加上外围对每个数据的遍历，复杂度O(n^2)，十万数据量必然超时。

所以，问题转化为——找到一个时间复杂度为O(logn)或O(1)的方法得到区间不重复的数字个数

树状数组可以用来统计区间上的‘可加’属性，查询和更新的复杂度都是O(logn)，这里我们把首次出现的数，直接更新add(i,1),表示a[i]出现，等之后再次遇到，叉掉上次的记录即add(lasti,-1) 再add(i,1) 永远只记录当前最新的那个数。

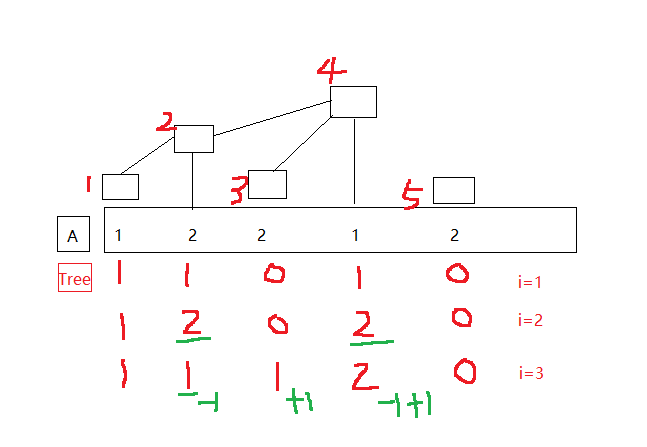
• 细节，因为单个数据可以到1e9，所以不能用flag[x]标记是否出现（数组开不了那么大）

c++

#include<iostream>
#include<unordered_map>

#define ffor(i,s,e) for(int i=s;i<e;i++)
using namespace std;


const int N=100010;
int a[N];
int n;
unordered_map<int,int> idx;


int tr[N];

int lowbit(int x){
    return x&(-x);
}

void add(int start,int x){//从start到n路上每个值增加x
    for(int i=start;i<=n;i+=lowbit(i)) tr[i]+=x;
}

int query(int pos){//求A1到Apos上可加属性的和
    int ans=0;
    for(int i=pos;i>0;i-=lowbit(i)) ans+=tr[i];
    return ans;
}

int main(){
    cin>>n;

    ffor(i,1,n+1) {
        scanf("%d",&a[i]);

        if(idx.find(a[i])==idx.end()){
            idx[a[i]]=i;
            add(i,1);//a[i]出现一次
            a[i]=-a[i];
        }else{
            int lasti=idx[a[i]];
            idx[a[i]]=i;//在更新ai之前赋值
            add(lasti,-1);//忽略掉上次出现
            add(i,1);
            a[i]=query(i-1)-query(lasti);
        }

    }

    ffor(i,1,n+1) printf("%d ",a[i]);
    return 0;


}