一棵二叉搜索树，Binary Search Tree——BST，和它的镜像二叉树，前、后序遍历有关系：
二叉搜索树的前序遍历 等同于 镜像树的后序遍历。
再精炼一些就是：原先 = 镜后
原来那棵树的先序遍历 = 镜像那棵树的后序遍历。

另外，原后 = 镜先也是自然成立的。

不过上述结论在本题中似乎没用到，只是我自己做题时以为有用，才去看了一下它们有什么关系。

然后说一下解题思路吧：

输入的是前序遍历，要求输出后序遍历。
先假设这个树是二叉搜索树，不是镜像树，为了方便讨论而已。

前序遍历的第一个数就是树根，那么之后需要把树根的左子树和右子树找出来。我们想一下，对BST（二叉搜索树）进行前序遍历，先输出根，然后对左子树重复前序遍历，然后对右子树重复前序遍历。（这其实就是一般数据结构教材中的定义）
那么输入的前序遍历中，肯定第一个数字是根，紧接着有一坨是左子树，剩下那一坨是右子树。所以找到那一坨左子树和那一坨右子树的分界点，然后递归地再对那坨左子树和那坨右子树进行相同的操作，就可以把这棵BST的结构搞清了。

所以哪一坨是左子树？怎么找？ 别忘了，这是BST，根的左子树都是比它数值小的（<），右子树都是比它数值大或相等的（>=）。而且左子树那一坨肯定在靠左的部分，右子树那一坨就是剩下右边的部分（因为前序遍历肯定是左子树先输出完了才输出右子树，所以左子树那一坨先输出，就是在输入中靠左）。所以要找左子树那一坨，就从左往右找，找到第一个比根大或相等的数值，那这个数值其实就是左、右子树的分界（这个数是右子树的一部分，因为这个数比根大或相等）。

接下来要更严谨地讨论其他可能的情况：这是镜像树；这既不是BST，也不是镜像树。
如果这是镜像树，那么根的左子树都是比根大或者相等的，右子树都是比根小的。那这样怎么找到哪一坨是左子树呢？自然还是从左往右，找到第一个比根小的数值，这个数值是右子树的一部分。

如果不是BST，也不是镜像树呢？
那这棵树肯定违反了BST的规定，也就是这棵树里边有一个数值，它本来应该在左边，但是跑到了右边。（或者本应在右边，跑到了左边）
假设这棵BST的某个数值本应在右边，但跑到了左边。也就是这个数值比根大或相等，按照BST的定义应该在右边，但跑到了左边。
如果我们继续按照从左往右找第一个大于或者等于根的数值，把它当作左、右子树的分界点，那找到的肯定是这个放错位置了的数值。

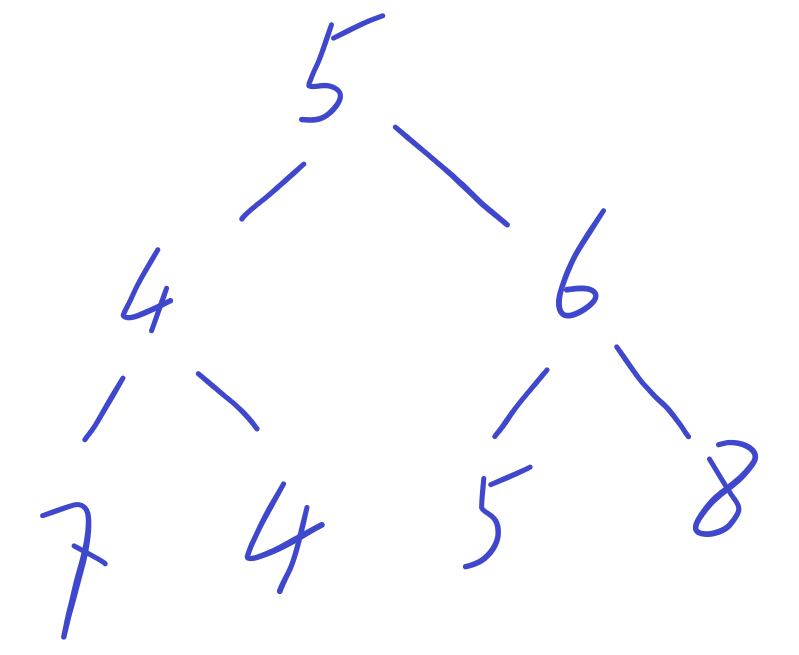
如上图，最左下角那个数字是7，应该在右子树，但跑到了左子树，这样前序遍历就变成了：
5 4 7 4 6 5 8
这样我们找左右子树的边界就会把7当作边界，所以怎么办呢？我们又不知道输入的序列一定是BST或者镜像树。其实这里可以从左往右找左子树一坨，也可以从右往左找右子树一坨，也可以同时从左往右，从右往左，左右子树两坨一起找。
如果是BST，那么从左往右找和从右往左找，找到的左右两坨树的分界点是相邻的，并且左子树最后一个元素的下标加1就是右子树第一个元素的下标。
为方便讨论，命名变量：
输入数组的边界：[l,r]
lc：左子树最后一个元素的下标。（取 left child首字母）
rc：右子树第一个元素的下标。（取 right child首字母）

讨论怎么找到lc：

可以从左往右找，左子树最后一个元素是小于根的，再下一个元素就大于或等于根了，所以就判断下标lc的下一个元素如果>=根，那么lc就停止移动，否则，lc = lc + 1;
同时，lc <= r也是必要的限制条件。

也可以从右往左找，右子树在输入数组靠右的部分，所以从右往左可以理解为穿越了右子树一坨，然后到了左子树的最右边。所以如果下标lc的数值比根大或相等，lc要减1；如果下标lc的数值比根小，说明lc成功穿越了右子树一坨，到达了边界。同时，lc > l是必要的限制条件。

我觉得第二种方法比较舒服，因为第一种是需要判断lc指向的数值的下一个元素。第一种是lc穿越左子树一坨，找左子树边界，所以要判断它的下一个元素，只有下一个元素是右子树的元素了，当前的元素才是左子树的边界。
而第二种是lc穿越右子树一坨，只要它一到达左子树，那就是左子树边界。因为它是从右往左穿越边界的，穿过了右边，到达了左边后的第一个位置就是左子树边界。

那么rc的找法也有上面两种。

另外，如果是镜像树，符号是和BST相反就可以了。
举个例子：找lc，从左往右找，左子树一坨是大于等于根的，所以如果下标lc的下一个数值小于根了，那么lc就停止增加。

最后，比较重要的一点，上述内容只是分清了左右子树的边界，假设在定义了函数f，在f中完成上述动作，接下来是递归地对左右子树调用f函数。紧接着，根入队。
为什么呢？因为题目要求输出后序遍历，数据结构教材上是怎么说的呢？先递归地对左子树进行后序遍历，再递归地对右子树进行后序遍历，然后输出根。
所以这里就是先递归地对左子树调用f函数，再递归地对右子树调用f函数，然后根入队（只要保存起来就好了，可以用vector，queue等等）。

如果题目给的输入的确是BST或者镜像树，那么从前至后输出队列中的元素就是后序遍历了。

代码中，先按照BST调用一下f函数，判断队列中元素个数是否为n，如果不为n，说明在函数里找左右子树边界时发现两个边界不统一，退出了。
那么就再按照镜像树调用一次f函数，再判断队列元素是否为n，如果还不是，那就说明不是BST也不是镜像树。
如果为n，按序输出队列中元素。

记得再次调用f时队列要清空。

以下是上述思路的代码，并非原创，只是详细的思路解释，以及自己的想法：实现某些功能是否有多种方法。

C++ 代码

#include <iostream>
#include <vector>
using namespace std;

const int maxn = 1005;
int a[maxn];
vector<int> q; //保存后序遍历结果

// 左右边界，以及是否为镜像树， fasle表示按照BST区分左右子树，true表示按照镜像树区分左右边界
void pre(int l, int r, bool isM) 
{
    if(l > r) return;
    int lc = r, rc = l + 1;
    //左子树一坨我从右往左找，右子树一坨我从左往右找

    if(!isM){
        while(lc > l && a[lc] >= a[l]) lc--;
        while(rc <= r && a[rc] < a[l]) rc++;
    }else{
        while(lc > l && a[lc] < a[l]) lc--;
        while(rc <= r && a[rc] >= a[l]) rc++;
    }
    if(lc + 1 != rc) return;
    pre(l+1, lc, isM);
    pre(rc, r, isM);
    q.push_back(a[l]);

}


int main()
{
    int n; cin >> n;
    for(int i = 0; i < n; ++i)
    {
        cin >> a[i];
    }

    pre(0, n-1, 0);
    if(q.size() != n){
        q.clear();
        pre(0, n-1, 1);
    }
    if(q.size() != n) cout << "NO";
    else{
        cout << "YES\n";
        for(int i = 0; i < n; ++i)
            cout << q[i] << " ";
    }



    return 0;
}