分析

• 本题的考点：KMP。

• KMP算法分析如下图：

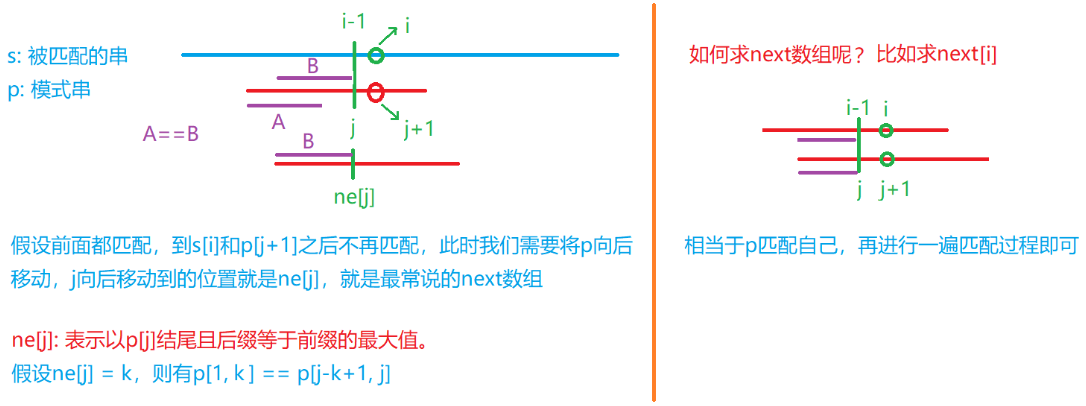
• 本题还可以调用对应API解决。

代码

• C++

class Solution {
public:
    int strStr(string haystack, string needle) {

        if (needle.empty()) return 0;
        if (needle.size() > haystack.size()) return -1;

        int m = haystack.size(), n = needle.size();
        string s = ' ' + haystack, p = ' ' + needle;
        vector<int> ne(n + 10, 0);
        for (int i = 2, j = 0; i <= n; i++) {
            while (j && p[i] != p[j + 1]) j = ne[j];
            if (p[i] == p[j + 1]) j++;
            ne[i] = j;
        }

        for (int i = 1, j = 0; i <= m; i++) {
            while (j && s[i] != p[j + 1]) j = ne[j];
            if (s[i] == p[j + 1]) j++;
            if (j == n) return i - n;
        }
        return -1;
    }
};

class Solution {
public:
    int strStr(string haystack, string needle) {
        return haystack.find(needle);
    }
};

• Java

class Solution {
    public int strStr(String haystack, String needle) {

        if (needle == null || needle.length() == 0) return 0;
        if (needle.length() > haystack.length()) return -1;

        int m = haystack.length(), n = needle.length();
        char[] s = (" " + haystack).toCharArray(), p = (" " + needle).toCharArray();

        int[] ne = new int[n + 10];
        for (int i = 2, j = 0; i <= n; i++) {
            while (j != 0 && p[i] != p[j + 1]) j = ne[j];
            if (p[i] == p[j + 1]) j++;
            ne[i] = j;
        }

        for (int i = 1, j = 0; i <= m; i++) {
            while (j != 0 && s[i] != p[j + 1]) j = ne[j];
            if (s[i] == p[j + 1]) j++;
            if (j == n) return i - n;
        }
        return -1;
    }
}

class Solution {
    public int strStr(String haystack, String needle) {
        return haystack.indexOf(needle);
    }
}

时空复杂度分析

• 时间复杂度：$O(m)$，m为被匹配的串长度。

• 空间复杂度：$O(n)$，n为模式串长度。