分析

• 本题的考点：动态规划。

• 这一题十分类似于最长上升子序列问题。

• 首先对数据进行排序，若$a[1]、a[2]、…、a[k-1]、a[k]$是答案，且是递增的，则一定有a[i] | a[i+1]（$1 \le i < k$）。反之如果我们已知a[i] | a[i+1]（$1 \le i < k$），能否推出从中任意选出两个元素都有较小的元素能整除较大的元素呢？这是可以得到的，因为整除具有传递性。

• 根据上述分析，我们可以使用动态规划求解，分析如下：

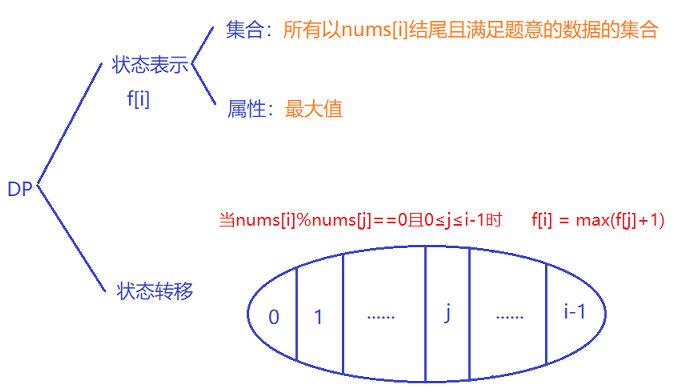
代码

• C++

class Solution {
public:
    vector<int> largestDivisibleSubset(vector<int> &nums) {

        sort(nums.begin(), nums.end());
        int n = nums.size();
        vector<int> f(n);
        int k = 0;  // 记录f最大时的下标，即f[k]最大
        for (int i = 0; i < n; i++) {
            f[i] = 1;
            for (int j = i - 1; j >= 0; j--)
                if (nums[i] % nums[j] == 0)
                    f[i] = max(f[i], f[j] + 1);
            if (f[k] < f[i]) k = i;
        }

        // 反向递推出答案
        vector<int> res(1, nums[k]);
        while (f[k] > 1) {
            for (int i = 0; i < k; i++)
                if (nums[k] % nums[i] == 0 && f[k] == f[i] + 1) {
                    res.push_back(nums[i]);
                    k = i;
                    break;
                }
        }
        return res;
    }
};

• Java

class Solution {
    public List<Integer> largestDivisibleSubset(int[] nums) {

        Arrays.sort(nums);
        int n = nums.length;
        int[] f = new int[n];
        int k = 0;  // 记录f最大时的下标，即f[k]最大
        for (int i = 0; i < n; i++) {
            f[i] = 1;
            for (int j = i - 1; j >= 0; j--)
                if (nums[i] % nums[j] == 0)
                    f[i] = Math.max(f[i], f[j] + 1);
            if (f[k] < f[i]) k = i;
        }

        // 反向递推出答案
        List<Integer> res = new ArrayList<>();
        res.add(nums[k]);
        while (f[k] > 1) {
            for (int i = 0; i < k; i++)
                if (nums[k] % nums[i] == 0 && f[k] == f[i] + 1) {
                    res.add(nums[i]);
                    k = i;
                    break;
                }
        }
        return res;
    }
}

时空复杂度分析

• 时间复杂度：$O(n^2)$，n为数组长度。计算状态转移时两层循环。

• 空间复杂度：$O(n)$，n为数组长度。