• 用 $\text{root}[\cdots]$ 数组来定位每个根节点，不妨设 $\text{trie}$ 中字符集合为 $C$，全体字符集为 $A$
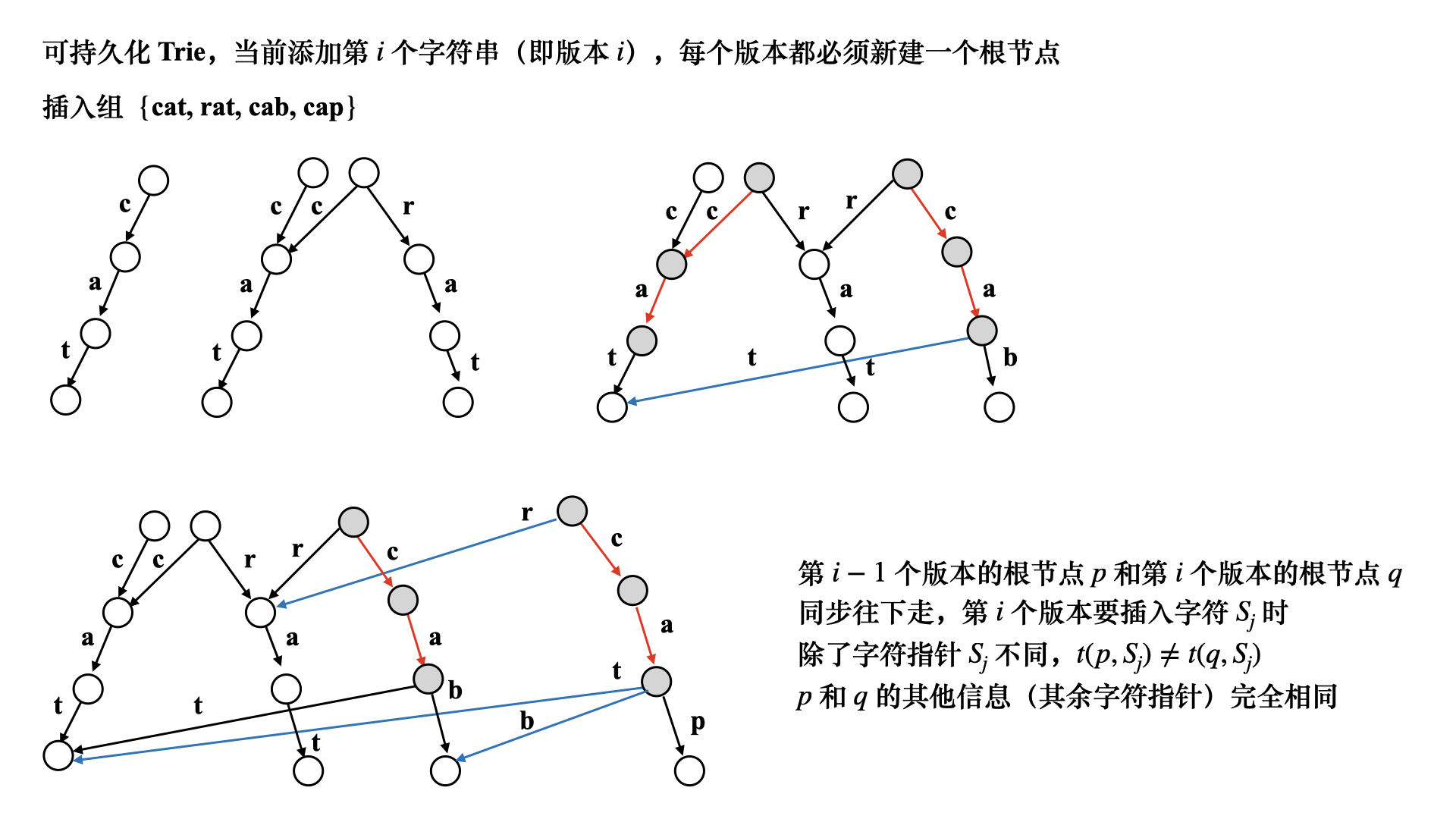
  当前插入第 $i$ 个字符串，即执行第 $i$ 个版本，$p \leftarrow \text{root}(i-1)$

• 新建一个节点 $q$，即 $q = root(i) = ++tot$，假设当前插入字符 $S_j$

• 如果 $p \neq 0$，对于 $\forall c \in \{C\}, \ c \neq S_j$，令 $t(q, c) \leftarrow t(p, c)$
  （这一步可以检查 $\forall c \in \{A\}$ 全体字符集，令 $t(q, c) \leftarrow t(p, c)$，因为下一步 $t(q, S_j)$ 会重新定位到新开的节点上）

• 新建一个节点，令 $t(q, S_j) = ++tot$，即除了 $S_j$ 指针不同外，$p, q$ 的其余信息完全相同

• $p \leftarrow t(p, S_j), q \leftarrow t(q, S_j), j \leftarrow j+1$ 直到字符串结尾

• 可以类似引入一个异或前缀和的概念

$$ \bigoplus_{i = p}^{n} a_p = S_n \oplus S_{p-1} $$

• 对于添加操作，很简单 $S_{n+1} = S_n \oplus x, \ n = n+1$

• 如果令 $p’ = p-1, \ l-1 \leqslant p’ \leqslant r-1$，询问操作实际上就是令 $val = x \oplus S_n$
  求一个位置 $p$，满足 $l-1 \leqslant p \leqslant r-1$，使得 $S_p \oplus val$ 最大
  这个问题如果没有 $p \in [l-1, r-1]$ 的限制，就是最大异或和问题

• 对于 $p \leqslant r-1$，可以借鉴主席树思想，对 $\text{trie}$ 进行可持久化，在第 $r-1$ 个版本
  即 $\text{root}(r-1)$ 中查询最大异或和路径
  （$p = \text{root}(r-1)$，从高位到低位尽可能沿着和 $val$ 相反的位走）

• 对于 $p \geqslant l-1$，只要保证异或和路径上所经过点的时间戳 $\geqslant l-1$ 即可
  对于插入操作 $\text{insert}(pre, p, i)$ 表示插入第 $i$ 个字符串
  $k$ 从高位到低位遍历，此时第 $k$ 位的字符为 $c = S_i >> k \& 1$

• 如果 $pre \neq 0$，令 $t(p, c\oplus 1) \leftarrow t(pre, c\oplus 1)$

• $t(p, c) = ++tot$，于此同时标记节点时间戳 $dfn(p) = i$，然后和主席树一样同步往下走
  $p \leftarrow t(p, c), \ pre \leftarrow t(pre, c), \textbf{then} \ dfn(p) = i$

const int N = 600000 + 5;
const int maxn = N * 25;
int n, m, s[N], root[N];

class Trie {
public:
    int t[maxn][2], dfn[maxn];
    int tot;

    Trie() {
        tot = 0;
        memset(t, 0, sizeof 0);
        memset(dfn, 0, sizeof 0);
        dfn[0] = -1;
    }

    void insert(int pre, int p, int ver) {
        dfn[p] = ver;
        for (int k = 25; k >= 0; k--) {
            int c = s[ver] >> k & 1;
            if (pre) t[p][c^1] = t[pre][c^1];
            t[p][c] = ++tot;
            p = t[p][c], pre = t[pre][c];
            dfn[p] = ver;
        }
    }

    int ask(int p, int val, int lim) {
        for (int k = 25; k >= 0; k--) {
            int c = val >> k & 1;
            if (dfn[ t[p][c^1] ] >= lim) p = t[p][c^1];
            else p = t[p][c];
        }
        return s[dfn[p]] ^ val;
    }
} trie;

int main() {
    freopen("input.txt", "r", stdin);
    cin >> n >> m;

    // init
    for (int i = 1; i <= n; i++) {
        int x;
        scanf("%d", &x);
        s[i] = s[i-1] ^ x;
        root[i] = ++trie.tot;
        trie.insert(root[i-1], root[i], i);
    }
    while (m--) {
        char cmd[2];
        scanf("%s", cmd);
        if (cmd[0] == 'A') {
            int x;
            scanf("%d", &x);
            root[++n] = ++trie.tot;
            s[n] = s[n-1] ^ x;
            trie.insert(root[n-1], root[n], n);
        }
        else {
            int l, r, x;
            scanf("%d%d%d", &l, &r, &x);
            int res = trie.ask(root[r-1], s[n]^x, l-1);
            printf("%d\n", res);
        }
    }
}