分析

• 本题的考点：动态规划。

• 这一题和完全背包问题十分类似，关于背包问题可以参考：背包九讲。但是和完全背包不同，不同点有两点：（1）这一题要求所选数据之和正好为target；（2）这一题数据相同但是排列不同的序列认为是不同的结果，例如1, 3和3, 1认为是不同的结果。

• 本题的分析如下：

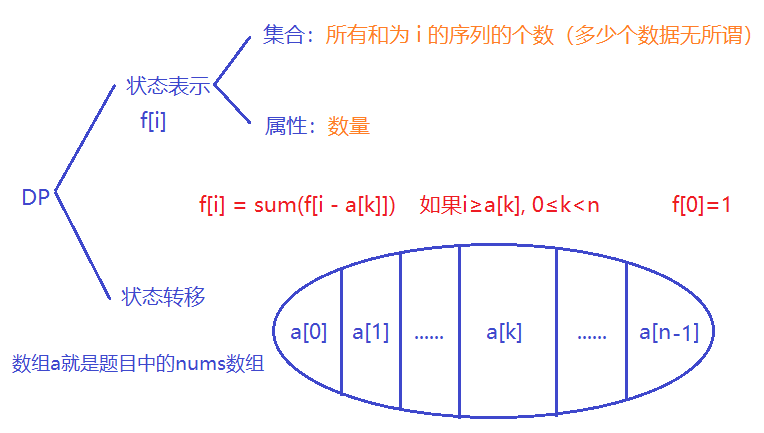
代码

• C++

class Solution {
public:
    int combinationSum4(vector<int>& nums, int m) {

        int n = nums.size();
        vector<long long> f(m + 1);  // 中间过程int会溢出
        f[0] = 1;  // 什么都不选也是一种方案
        for (int i = 0; i <= m; i++)
            for (int v : nums)
                if (i >= v)
                    f[i] = (f[i] + f[i - v]) % INT_MAX;
        return f[m];
    }
};

• Java

class Solution {
    public int combinationSum4(int[] nums, int m) {

        int n = nums.length;
        int[] f = new int[m + 1];  // 不需要考虑溢出问题, lc提交能通过
        f[0] = 1;
        for (int i = 0; i <= m; i++)
            for (int v : nums)
                if (i >= v)
                    f[i] += f[i - v];
        return f[m];
    }
}

时空复杂度分析

• 时间复杂度：$O(n \times m)$，n为数组长度，m为需要组合出的数。

• 空间复杂度：$O(m)$，m为需要组合出的数。