题目描述

小扣有一个根结点为 root 的二叉树模型，初始所有结点均为白色，可以用蓝色染料给模型结点染色，模型的每个结点有一个 val 价值。小扣出于美观考虑，希望最后二叉树上每个蓝色相连部分的结点个数不能超过 k 个，求所有染成蓝色的结点价值总和最大是多少？

样例

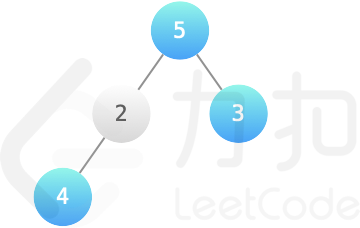
输入：root = [5,2,3,4], k = 2
输出：12
解释：结点 5、3、4 染成蓝色，获得最大的价值 5+3+4=12

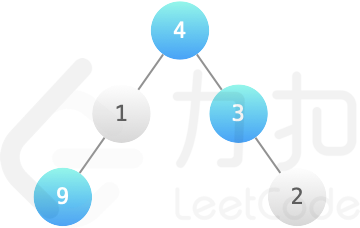
输入：root = [4,1,3,9,null,null,2], k = 2
输出：16
解释：结点 4、3、9 染成蓝色，获得最大的价值 4+3+9=16

限制

• 1 <= k <= 10
• 1 <= val <= 10000
• 1 <= 结点数量 <= 10000

算法

(动态规划) $O(nk^2)$

1. 设 $f(root, j)$ 为以 $root$ 为根节点的子树，且和结点 $root$ 相连的连通块的大小为 $j$ 时，符合要求的最大价值。
2. 初始时，$f(nul, 0) = 0$，对 $1 \le j \le k$，$f(nul, j) = -\infty$。
3. 转移时，有两种选择，一种是不选择结点 $root$，一种是选择结点 $root$。
4. 对于不选择结点 $root$，则转移 $f(root, 0) = \max(f(l, j)) + \max(f(r, j))$，即找到左右子树中的 $f(l, j)$ 和 $f(r, j)$ 的最大值求和。
5. 对于选择结点 $root$，则对于当前连通块大小为 $i$ 时，枚举左子树的连通块大小为 $j$，则转移 $f(root, i) = \max(f(root, i), f(l, j) + f(r, i - j - 1) + root.val)$。
6. 最终答案为整棵树根结点中的最大值。

时间复杂度

• 对于每个结点，需要 $O(k^2)$ 的时间处理转移，故总时间复杂度为 $O(nk^2)$。

空间复杂度

• 需要 $O(nk)$ 的空间复杂度存储递归的系统栈。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {

#define INF 1000000000

private:
    vector<int> solve(TreeNode *root, int k) {
        vector<int> v(k + 1, -INF);

        if (root == NULL) {
            v[0] = 0;
            return v;
        }

        vector<int> l = solve(root->left, k);
        vector<int> r = solve(root->right, k);

        int maxl = -INF, maxr = -INF;
        for (int i = 0; i <= k; i++) {
            maxl = max(maxl, l[i]);
            maxr = max(maxr, r[i]);
        }

        v[0] = maxl + maxr;

        for (int i = 0; i <= k; i++)
            for (int j = 0; j <= i - 1; j++)
                v[i] = max(v[i], l[j] + r[i - j - 1] + root->val);

        return v;
    }

public:
    int maxValue(TreeNode* root, int k) {
        vector<int> v = solve(root, k);

        int ans = 0;
        for (int i = 0; i <= k; i++)
            ans = max(ans, v[i]);

        return ans;
    }
};