分析

• 本题的考点：数组。

• 核心思路：我们求出每个位置能存储的水量，最后加到一起就可以得到答案，如下图五个地方的水量相加即可：

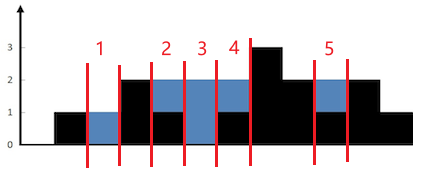
• 那么如何求解每个位置可以存放的雨水？我们可以预先处理处两个数组left_max和right_max。left_max[i]表示height[0]~height[i]中最高的柱子，right_max[i]表示height[i]~height[n-1]中最高的柱子。

• 则对于位置i，可以存储的雨水为：min(left_max[i], right_max[i]) - height[i]。

• 这一题其实是Leetcode 0407 接雨水 II一个简单版本，本题是二维版本，Leetcode 0407 接雨水 II是三维版本。

代码

• C++

class Solution {
public:
    int trap(vector<int> &height) {

        int n = height.size();
        if (n == 0) return 0;

        vector<int> left_max(n), right_max(n);

        left_max[0] = height[0];
        for (int i = 1; i < n; i++) left_max[i] = max(left_max[i - 1], height[i]);
        right_max[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i--) right_max[i] = max(right_max[i + 1], height[i]);

        int res = 0;
        for (int i = 0; i < n; i++) res += min(left_max[i], right_max[i]) - height[i];

        return res;
    }
};

• Java

class Solution {
    public int trap(int[] height) {

        int n = height.length;
        if (n == 0) return 0;

        int[] left_max = new int[n], right_max = new int[n];

        left_max[0] = height[0];
        for (int i = 1; i < n; i++) left_max[i] = Math.max(left_max[i - 1], height[i]);
        right_max[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i--) right_max[i] = Math.max(right_max[i + 1], height[i]);

        int res = 0;
        for (int i = 0; i < n; i++) res += Math.min(left_max[i], right_max[i]) - height[i];

        return res;
    }
}

时空复杂度分析

• 时间复杂度：$O(n)$。n为数组长度。

• 空间复杂度：$O(n)$。n为数组长度。