分析

• 本题的考点：递归回溯。

• 递归过程中我们依次枚举每行，然后看这一行中皇后可以放置在哪个位置。并在过程中记录方案数。

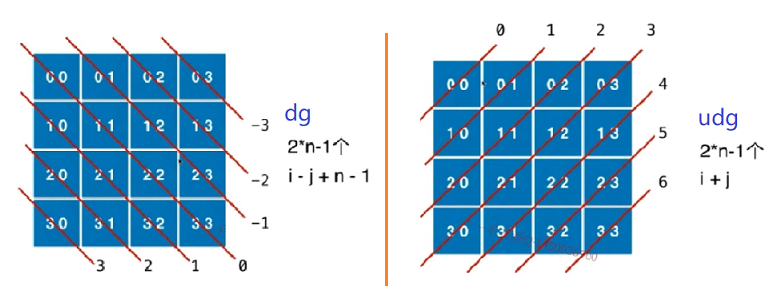
• 对于当前枚举的某行u，如果判断该行中的第i列是否可以放置一个皇后呢？可以使用三个数组col、dg、udg表示列、左上到右下斜线、右上到左下斜线中是否放置了皇后。坐标转化关系如下：

代码

• C++

class Solution {
public:
    int n;
    vector<bool> col, dg, udg;

    int totalNQueens(int _n) {
        n = _n;
        col = vector<bool>(n);
        dg = udg = vector<bool>(n * 2 - 1);

        return dfs(0);
    }

    // 返回方案数
    int dfs(int u) {
        if (u == n) return 1;

        int res = 0;
        for (int i = 0; i < n; i ++ ) {
            if (!col[i] && !dg[u - i + n - 1] && !udg[u + i]) {
                col[i] = dg[u - i + n - 1] = udg[u + i] = true;
                res += dfs(u + 1);
                col[i] = dg[u - i + n - 1] = udg[u + i] = false;
            }
        }
        return res;
    }
};

• Java

class Solution {

    int n;
    boolean[] col, dg, udg;

    public int totalNQueens(int _n) {

        n = _n;
        col = new boolean[n];
        dg = new boolean[n * 2 - 1]; udg = new boolean[n * 2 - 1];

        return dfs(0);
    }

    // 返回方案数
    private int dfs(int u) {
        if (u == n) return 1;

        int res = 0;
        for (int i = 0; i < n; i++) 
            if (!col[i] && !dg[u - i + n - 1] && !udg[u + i]) {
                col[i] = dg[u - i + n - 1] = udg[u + i] = true;
                res += dfs(u + 1);
                col[i] = dg[u - i + n - 1] = udg[u + i] = false;
            }
        return res;
    }
}

时空复杂度分析

• 时间复杂度：指数级别的。

• 空间复杂度：和递归深度有关。