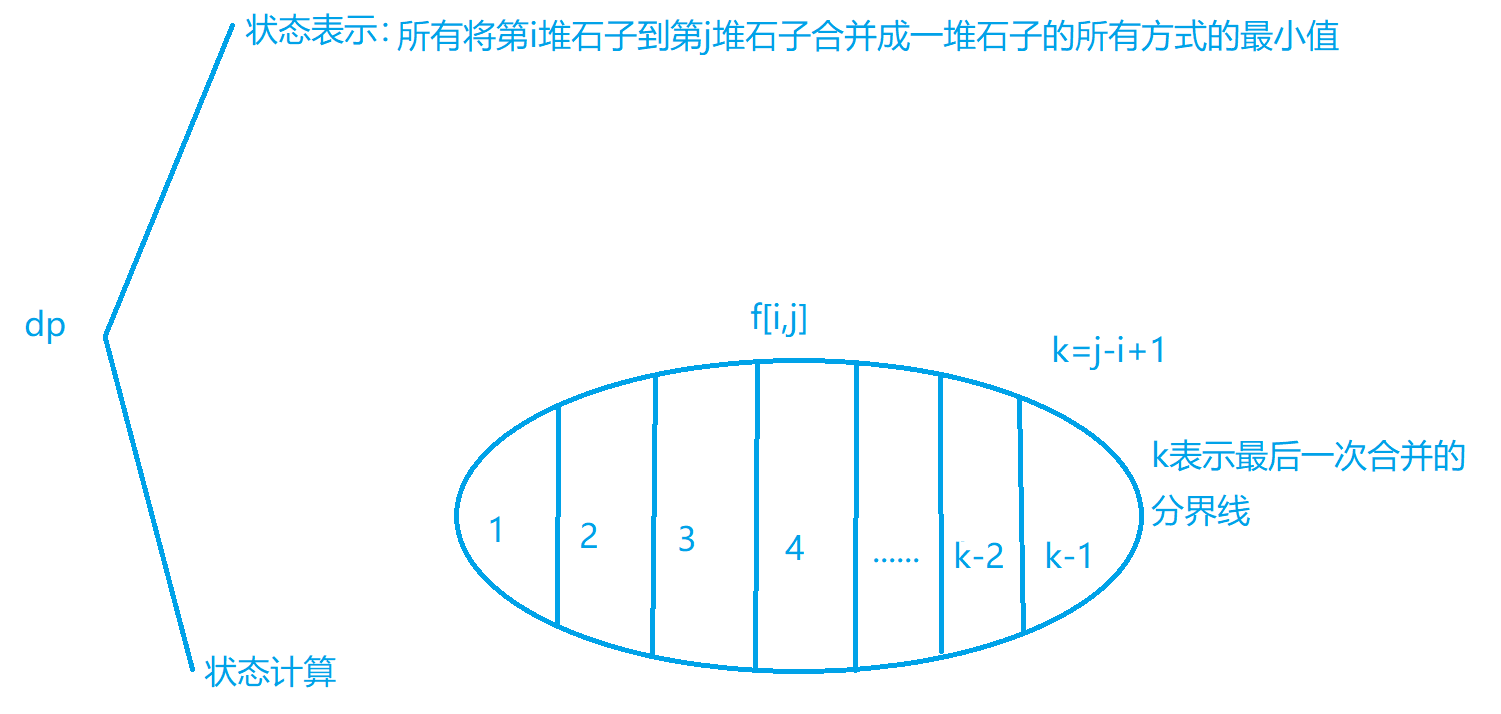
题目描述

设有 N 堆石子排成一排，其编号为 1，2，3，…，N。

每堆石子有一定的质量，可以用一个整数来描述，现在要将这 N 堆石子合并成为一堆。

每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有 4 堆石子分别为 1 3 5 2， 我们可以先合并 1、2 堆，代价为 4，得到 4 5 2， 又合并 1，2 堆，代价为 9，得到 9 2 ，再合并得到 11，总代价为 4+9+11=24；

如果第二步是先合并 2，3 堆，则代价为 7，得到 4 7，最后一次合并代价为 11，总代价为 4+7+11=22。

问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

样例

输入样例：
4
1 3 5 2
输出样例：
22

#include<iostream>
using namespace std;
const int N=310;
int s[N];
int f[N][N];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&s[i]);
        s[i]+=s[i-1];
    }

    for(int len=2;len<=n;len++)
        for(int i=1;i+len-1<=n;i++)
        {
            int l=i,r=i+len-1;
            f[l][r]=1e9;//注意初始化
            for(int k=l;k<r;k++)
                f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
        }
    cout<<f[1][n]<<endl;
    return 0;
}