题目描述

给你两棵二叉树：root1 和 root2。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意：合并过程必须从两个树的根节点开始。

样例

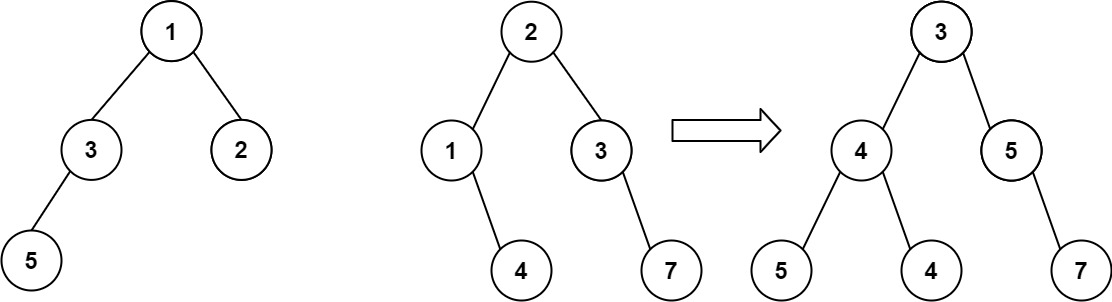
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

限制

• 两棵树中的节点数目在范围 [0, 2000] 内。
• -10^4 <= Node.val <= 10^4

算法

(递归) $O(n + m)$

1. 主要思路是以第一棵树为基准，将第二棵树往第一课树上添加。
2. 从根结点开始递归，递归时分为四种情况：$t_1$ 和 $t_2$ 均为空，则返回空；$t_1$ 为空，$t_2$ 不为空，则返回 $t_2$；$t_1$ 不为空，$t_2$ 为空，则返回 $t_1$；$t_1$ 和 $t_2$ 均为空，则分别递归左子树和右子树，令 $t_1$ 的左儿子指向递归返回的左子树，$t_1$ 的右儿子指向递归返回的右子树，最后返回 $t_1$。

时间复杂度

• 每个结点最多遍历一次，故时间复杂度为 $O(n + m)$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        if (!t1 && !t2)
            return NULL;
        if (!t1 && t2)
            return t2;
        if (t1 && !t2)
            return t1;
        t1 -> val += t2 -> val;
        t1 -> left = mergeTrees(t1 -> left, t2 -> left);
        t1 -> right = mergeTrees(t1 -> right, t2 -> right);
        return t1;
    }
};